This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Vertex Coloring”.
1. Which of the following is not a type of graph in computer science?
a) undirected graph
b) bar graph
c) directed graph
d) weighted graph
View Answer
Explanation: According to the graph theory a graph is the collection of dots and lines. A bar graph is not a type of graph in computer science.
2. What is vertex coloring of a graph?
a) A condition where any two vertices having a common edge should not have same color
b) A condition where any two vertices having a common edge should always have same color
c) A condition where all vertices should have a different color
d) A condition where all vertices should have same color
View Answer
Explanation: The condition for vertex coloring of a graph is that two vertices which share a common edge should not have the same color. If it uses k colors in the process then it is called k coloring of graph.
3. How many edges will a tree consisting of N nodes have?
a) Log(N)
b) N
c) N – 1
d) N + 1
View Answer
Explanation: In order to have a fully connected tree it must have N-1 edges. So the correct answer will be N-1.
4. Minimum number of unique colors required for vertex coloring of a graph is called?
a) vertex matching
b) chromatic index
c) chromatic number
d) color number
View Answer
Explanation: The minimum number of colors required for proper vertex coloring of graph is called chromatic number whereas the minimum number of colors required for proper edge coloring of graph is called chromatic index of a graph.
5. How many unique colors will be required for proper vertex coloring of an empty graph having n vertices?
a) 0
b) 1
c) 2
d) n
View Answer
Explanation: An empty graph is a graph without any edges. So the number of unique colors required for proper coloring of the graph will be 1.
6. How many unique colors will be required for proper vertex coloring of a bipartite graph having n vertices?
a) 0
b) 1
c) 2
d) n
View Answer
Explanation: A bipartite graph is a graph such that no two vertices of the same set are adjacent to each other. So the number of unique colors required for proper coloring of the graph will be 2.
7. Which of the following is an NP complete problem?
a) Hamiltonian cycle
b) Travelling salesman problem
c) Calculating chromatic number of graph
d) Finding maximum element in an array
View Answer
Explanation: Calculating the chromatic number of a graph is an NP complete problem as a chromatic number of an arbitrary graph cannot be determined by using any convenient method.
8. How many unique colors will be required for proper vertex coloring of a line graph having n vertices?
a) 0
b) 1
c) 2
d) n
View Answer
Explanation: A line graph of a simple graph is obtained by connecting two vertices with an edge. So the number of unique colors required for proper coloring of the graph will be n.
9. How many unique colors will be required for proper vertex coloring of a complete graph having n vertices?
a) 0
b) 1
c) n
d) n!
View Answer
Explanation: A complete graph is the one in which each vertex is directly connected with all other vertices with an edge. So the number of unique colors required for proper coloring of the graph will be n.
10. Minimum number of colors required for proper edge coloring of a graph is called?
a) Chromatic color
b) Chromatic index
c) Edge matching
d) Color number
View Answer
Explanation: The minimum number of colors required for proper edge coloring of graph is called chromatic index. It is also known as edge chromatic number.
11. What will be the chromatic number of the following graph?

a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: The given graph will only require 2 unique colors so that no two vertices connected by a common edge will have the same color. All nodes will have the same color except the central node.
12. How many unique colors will be required for vertex coloring of the following graph?
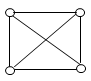
a) 2
b) 3
c) 4
d) 5
View Answer
Explanation: The given graph will require 4 unique colors so that no two vertices connected by a common edge will have the same color. So its chromatic number will be 4.
13. How many unique colors will be required for vertex coloring of the following graph?
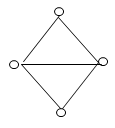
a) 2
b) 3
c) 4
d) 5
View Answer
Explanation: The given graph will require 3 unique colors because two diagonal vertex are connected to each other directly. So its chromatic number will be 3.
14. Vertex coloring and chromatic number are one and the same.
a) True
b) False
View Answer
Explanation: Vertex coloring of a graph is an assignment of colors to the vertices of a graph such that no two adjacent vertices have the same color. Whereas chromatic number refers to the minimum number of unique colors required for vertex coloring of the graph.
Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.
To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Data Structure MCQ
- Check Programming Books
- Apply for Computer Science Internship
- Check Design and Analysis of Algorithms Books
- Practice Programming MCQs
