This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Minimum Spanning Tree”.
1. Which of the following is false in the case of a spanning tree of a graph G?
a) It is tree that spans G
b) It is a subgraph of the G
c) It includes every vertex of the G
d) It can be either cyclic or acyclic
View Answer
Explanation: A graph can have many spanning trees. Each spanning tree of a graph G is a subgraph of the graph G, and spanning trees include every vertex of the gram. Spanning trees are always acyclic.
2. Every graph has only one minimum spanning tree.
a) True
b) False
View Answer
Explanation: Minimum spanning tree is a spanning tree with the lowest cost among all the spacing trees. Sum of all of the edges in the spanning tree is the cost of the spanning tree. There can be many minimum spanning trees for a given graph.
3. Consider a complete graph G with 4 vertices. The graph G has ____ spanning trees.
a) 15
b) 8
c) 16
d) 13
View Answer
Explanation: A graph can have many spanning trees. And a complete graph with n vertices has n(n-2) spanning trees. So, the complete graph with 4 vertices has 4(4-2) = 16 spanning trees.
4. The travelling salesman problem can be solved using _________
a) A spanning tree
b) A minimum spanning tree
c) Bellman – Ford algorithm
d) DFS traversal
View Answer
Explanation: In the travelling salesman problem we have to find the shortest possible route that visits every city exactly once and returns to the starting point for the given a set of cities. So, travelling salesman problem can be solved by contracting the minimum spanning tree.
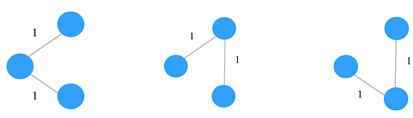
5. Consider the graph M with 3 vertices. Its adjacency matrix is shown below. Which of the following is true?
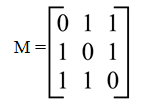
a) Graph M has no minimum spanning tree
b) Graph M has a unique minimum spanning trees of cost 2
c) Graph M has 3 distinct minimum spanning trees, each of cost 2
d) Graph M has 3 spanning trees of different costs
View Answer
Explanation: Here all non-diagonal elements in the adjacency matrix are 1. So, every vertex is connected every other vertex of the graph. And, so graph M has 3 distinct minimum spanning trees.
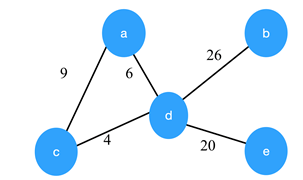
6. Consider a undirected graph G with vertices { A, B, C, D, E}. In graph G, every edge has distinct weight. Edge CD is edge with minimum weight and edge AB is edge with maximum weight. Then, which of the following is false?
a) Every minimum spanning tree of G must contain CD
b) If AB is in a minimum spanning tree, then its removal must disconnect G
c) No minimum spanning tree contains AB
d) G has a unique minimum spanning tree
View Answer
Explanation: Every MST will contain CD as it is smallest edge. So, Every minimum spanning tree of G must contain CD is true. And G has a unique minimum spanning tree is also true because the graph has edges with distinct weights. So, no minimum spanning tree contains AB is false.
7. If all the weights of the graph are positive, then the minimum spanning tree of the graph is a minimum cost subgraph.
a) True
b) False
View Answer
Explanation: A subgraph is a graph formed from a subset of the vertices and edges of the original graph. And the subset of vertices includes all endpoints of the subset of the edges. So, we can say MST of a graph is a subgraph when all weights in the original graph are positive.
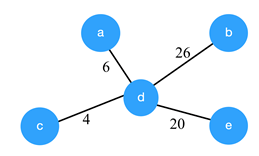
8. Consider the graph shown below. Which of the following are the edges in the MST of the given graph?
a) (a-c)(c-d)(d-b)(d-b)
b) (c-a)(a-d)(d-b)(d-e)
c) (a-d)(d-c)(d-b)(d-e)
d) (c-a)(a-d)(d-c)(d-b)(d-e)
View Answer
9. Which of the following is not the algorithm to find the minimum spanning tree of the given graph?
a) Boruvka’s algorithm
b) Prim’s algorithm
c) Kruskal’s algorithm
d) Bellman–Ford algorithm
View Answer
Explanation: The Boruvka’s algorithm, Prim’s algorithm and Kruskal’s algorithm are the algorithms that can be used to find the minimum spanning tree of the given graph.
The Bellman-Ford algorithm is used to find the shortest path from the single source to all other vertices.
10. Which of the following is false?
a) The spanning trees do not have any cycles
b) MST have n – 1 edges if the graph has n edges
c) Edge e belonging to a cut of the graph if has the weight smaller than any other edge in the same cut, then the edge e is present in all the MSTs of the graph
d) Removing one edge from the spanning tree will not make the graph disconnected
View Answer
Explanation: Every spanning tree has n – 1 edges if the graph has n edges and has no cycles. The MST follows the cut property, Edge e belonging to a cut of the graph if has the weight smaller than any other edge in the same cut, then the edge e is present in all the MSTs of the graph.
Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.
To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Programming MCQs
- Check Programming Books
- Check Computer Science Books
- Practice Data Structure MCQ
- Apply for Computer Science Internship