This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Maximum Flow Problem”.
1. What does Maximum flow problem involve?
a) finding a flow between source and sink that is maximum
b) finding a flow between source and sink that is minimum
c) finding the shortest path between source and sink
d) computing a minimum spanning tree
View Answer
Explanation: The maximum flow problem involves finding a feasible flow between a source and a sink in a network that is maximum and not minimum.
2. A network can have only one source and one sink.
a) False
b) True
View Answer
Explanation: A network can have only one source and one sink inorder to find the feasible flow in a weighted connected graph.
3. What is the source?
a) Vertex with no incoming edges
b) Vertex with no leaving edges
c) Centre vertex
d) Vertex with the least weight
View Answer
Explanation: Vertex with no incoming edges is called as a source. Vertex with no leaving edges is called as a sink.
4. Which algorithm is used to solve a maximum flow problem?
a) Prim’s algorithm
b) Kruskal’s algorithm
c) Dijkstra’s algorithm
d) Ford-Fulkerson algorithm
View Answer
Explanation: Ford-fulkerson algorithm is used to compute the maximum feasible flow between a source and a sink in a network.
5. Does Ford- Fulkerson algorithm use the idea of?
a) Naïve greedy algorithm approach
b) Residual graphs
c) Minimum cut
d) Minimum spanning tree
View Answer
Explanation: Ford-Fulkerson algorithm uses the idea of residual graphs which is an extension of naïve greedy approach allowing undo operations.
6. The first step in the naïve greedy algorithm is?
a) analysing the zero flow
b) calculating the maximum flow using trial and error
c) adding flows with higher values
d) reversing flow if required
View Answer
Explanation: The first step in the naïve greedy algorithm is to start with the zero flow followed by adding edges with higher values.
7. Under what condition can a vertex combine and distribute flow in any manner?
a) It may violate edge capacities
b) It should maintain flow conservation
c) The vertex should be a source vertex
d) The vertex should be a sink vertex
View Answer
Explanation: A vertex can combine and distribute flow in any manner but it should not violate edge capacities and it should maintain flow conservation.
8. Find the maximum flow from the following graph.
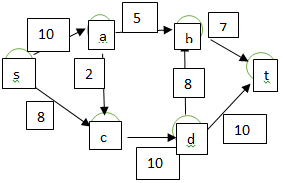
a) 22
b) 17
c) 15
d) 20
View Answer
Explanation: Initially, zero flow is computed. Then, computing flow= 7+1+5+2=15. Hence, maximum flow=15.
9. A simple acyclic path between source and sink which pass through only positive weighted edges is called?
a) augmenting path
b) critical path
c) residual path
d) maximum path
View Answer
Explanation: Augmenting path between source and sink is a simple path without cycles. Path consisting of zero slack edges is called critical path.
10. In what time can an augmented path be found?
a) O(|E| log |V|)
b) O(|E|)
c) O(|E|2)
d) O(|E|2 log |V|)
View Answer
Explanation: An augmenting path can be found in O(|E|) mathematically by an unweighted shortest path algorithm.
11. Dinic’s algorithm runs faster than the Ford-Fulkerson algorithm.
a) true
b) false
View Answer
Explanation: Dinic’s algorithm includes construction of level graphs and resLidual graphs and finding of augmenting paths along with blocking flow and is faster than the Ford-Fulkerson algorithm.
12. What is the running time of an unweighted shortest path algorithm whose augmenting path is the path with the least number of edges?
a) O(|E|)
b) O(|E||V|)
c) O(|E|2|V|)
d) O(|E| log |V|)
View Answer
Explanation: Each augmenting step takes O(|E|) using an unweighted shortest path algorithm yielding a O(|E|2|V|) bound on the running time.
13. Who is the formulator of Maximum flow problem?
a) Lester R. Ford and Delbert R. Fulkerson
b) T.E. Harris and F.S. Ross
c) Y.A. Dinitz
d) Kruskal
View Answer
Explanation: The first ever people to formulate Maximum flow problem were T.E. Harris and F.S. Ross. Lester R. Ford and Delbert R. Fulkerson formulated Ford- Fulkerson algorithm.
14. What is the running time of Dinic’s blocking flow algorithm?
a) O(V2E)
b) O(VE2)
c) O(V3)
d) O(E max |f|)
View Answer
Explanation: The running time of Dinic’s blocking flow algorithm is O(V2E). The running of Ford-Fulkerson algorithm is O(E max |f|).
15. How many constraints does flow have?
a) one
b) three
c) two
d) four
View Answer
Explanation: A flow is a mapping which follows two constraints- conservation of flows and capacity constraints.
Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.
To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Data Structure MCQ
- Practice Programming MCQs
- Practice Computer Science MCQs
- Check Design and Analysis of Algorithms Books
- Check Computer Science Books
