This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Fleury’s Algorithm”.
1. Fleury’s algorithm can be used to print which type of paths or circuits?
a) Hamiltonian
b) Eulerian
c) Directed path
d) Undirected path
View Answer
Explanation: In an undirected graph G, an eulerian circuit is a closed trail, which starts and ends at the same vertex. To find such a circuit in the given graph, fleury’s algorithm can be used. Before applying this algorithm, make sure that the given graph is connected.
2. What among the following is the basic idea of fleury’s algorithm?
a) Never travel across a bridge of untraveled part of the graph
b) Never travel across a bridge
c) Travel across the bridge of untraveled part, if there is no other choice
d) Travel across a bridge again over the traveled part of the graph
View Answer
Explanation: The basic idea of fleury’s algorithm is that the last edge we cross should be the bridge edge. Bridge edge is the edge, that connects two connected components of the graph. Hence, it should travel across the bridge of the untraveled part, only if there is no other alternative.
3. To find an eulerian cycle by fleury’s algorithm, from which vertex you should start if the graph has no odd vertices?
a) Vertex with degree 1
b) Any vertex of the graph
c) Vertex with the highest degree
d) Vertex with the lowest degree
View Answer
Explanation: The first step in fleury’s algorithm says that, if there are 2 odd degree vertices in the graph, always start with a vertex having an odd degree. But if there are no odd vertices in the graph, you can start with any of the vertex, which will give you an eulerian circuit.
4. Consider the fleury’s algorithm given below. Which of the following best suits the blank?
Graph must have 0 or 2 odd vertices if there are 0 odd vertices, start from any vertex if there are 2 odd vertices, start from any one of them follow any of the edge, always choose the ______________ repeat for all the edges of the graph
a) non-bridge over the bridge
b) bridge over non-bridge
c) adjacent edges
d) opposite edges
View Answer
Explanation: The idea of fleury’s algorithm is to cover the bridge edge as the last edge to be covered. The degree of all the vertices must be even or 0 or only 2 odd degree vertices. If there are no odd degree vertices, start from anywhere. If there are 2 odd vertices, start from any of these vertices. Starting traversing from any of the edges in such a way it shouldn’t divide the graph into two disconnected components. Hence, always choose the non-bridge edge over the bridge edge.
5. The fleury’s algorithm can be applied to a graph if the degree of all the vertices is even or two vertices with an odd degree.
a) True
b) False
View Answer
Explanation: In a graph, the number of odd degree vertices are always even. Fleury’s algorithm is used to find the eulerian circuit for the given graph. The graph will contain an euler circuit if and only if all the vertices of the graph has an even degree or 2 vertices of odd degree.
6. Consider the graph given below, print the eulerian circuit of the graph using fleury’s algorithm?
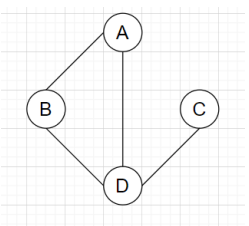
a) ABDC
b) DABDC
c) DABC
d) BADC
View Answer
Explanation: Eulerian circuit is a closed trail, which covers all the edges of the graph. In fleury’s algorithm we always start with the vertex having an odd degree if exists. If there are no odd degree vertices in the graph, we can start from anywhere. In the given graph, vertex D and C are the vertices having an odd degree. Always choose the edge which is non-bridge over bridge edge. Hence, this algorithm gives the eulerian tour D→A→B→D→C.
7. To find an eulerian circuit in the graph by fleury’s algorithm, always begin with the vertex having an odd degree.
a) True
b) False
View Answer
Explanation: Fleury’s algorithm to find an eulerian circuit in the given graph says that always start with vertices having an odd degree. Traverse through any edge, in such a way that the edge wouldn’t separate the graph and make it disconnected.
8. What is the time complexity of fleury’s algorithm?
a) O(V)
b) O(E)
c) O(V * E)
d) O((V + E)2)
View Answer
Explanation: Fleury’s algorithm is used to print eulerian path in a graph. In order to do so, we need to check whether each and every edge is bridge or not. To traverse through the graph which is stored in the form of adjacency list, O(V + E) time is required. At every edge DFS is performed to check if it is a bridge which requires O(V + E) time. Therefore, to print eulerian path using fleury’s algorithm, O((V + E)2) time is required.
Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.
To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Computer Science Internship
- Practice Programming MCQs
- Practice Data Structure MCQ
- Check Computer Science Books
- Check Design and Analysis of Algorithms Books
