This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Heap Sort – 2”.
1. Heap sort is an implementation of ____________ using a descending priority queue.
a) insertion sort
b) selection sort
c) bubble sort
d) merge sort
View Answer
Explanation: Heap sort is an implementation of selection sort using the input array as a heap representing a descending priority queue. Heap sort algorithm is divided into two phase. In first phase the max-heap is created and the second phase (selection phase) deletes the elements from the priority queue using siftdown operation.
2. Which one of the following is false?
a) Heap sort is an in-place algorithm
b) Heap sort has O(nlogn) average case time complexity
c) Heap sort is stable sort
d) Heap sort is a comparison-based sorting algorithm
View Answer
Explanation: Heap sort is a comparison based sorting algorithm and has time complexity O(nlogn) in the average case. Heap sort is an in-place algorithm as it needs O(1) of auxiliary space. Heap sort uses heap and operations on heap can change the relative order of items with the same key values. Therefore, Heap sort is not a stable sort.
3. The essential part of Heap sort is construction of max-heap. Consider the tree shown below, the node 24 violates the max-heap property. Once heapify procedure is applied to it, which position will it be in?
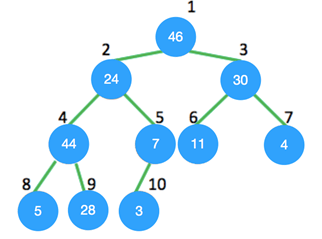
a) 4
b) 5
c) 8
d) 9
View Answer
Explanation: In max-heap element at each node is smaller than or equal to the element at its parent node. On applying the heapify procedure on item at position 2, it will be in position 9 as shown below.
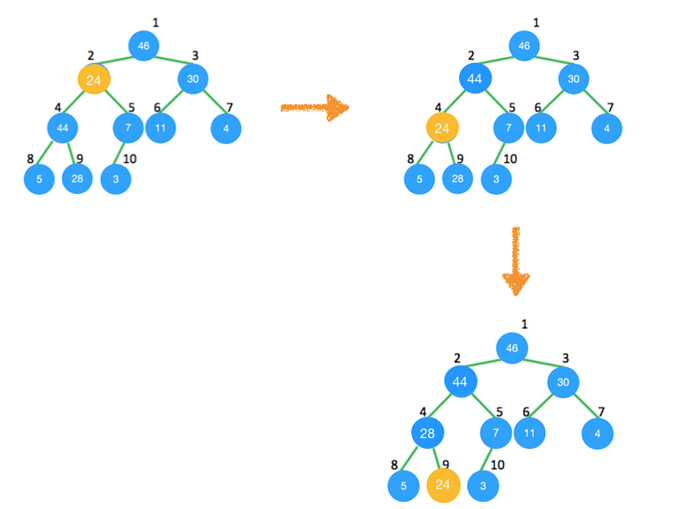
4. The descending heap property is ___________
a) A[Parent(i)] = A[i]
b) A[Parent(i)] <= A[i]
c) A[Parent(i)] >= A[i]
d) A[Parent(i)] > 2 * A[i]
View Answer
Explanation: The max-heap is also known as descending heap. Max-heap of size n is an almost complete binary tree of n nodes such that the element at each node is less than or equal to the element at its parent node.
5. What is its wort case time complexity of Heap sort?
a) O(nlogn)
b) O(n2logn)
c) O(n2)
d) O(n3)
View Answer
Explanation: In Heap sort, the call to procedure build_Max-heap takes O(n) time and each of O(n) calls to the function max_Heapify takes O(logn) time. So the worst case complexity of Heap sort is O(nlogn).
6. In average case Heap sort is as efficient as the Quick sort.
a) True
b) False
View Answer
Explanation: Quick sort is more efficient than Heap sort because experiments indicate that Heap sort requires twice as much time as Quick sort for randomly sorted input.
7. Choose the correct option to fill? X so that the code given below implements the Heap sort.
#include <stdio.h> void heapify(int arr[], int n, int i) { int largest = i; // Initialize largest as root int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 if (l < n && arr[l] > arr[largest]) largest = l; if (r < n && arr[r] > arr[largest]) largest = r; if (largest != i) { swap(arr[i], arr[largest]); heapify(arr, n, largest); } } void heapSort(int arr[], int n) { for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); for (int i=n-1; i>=0; i--) { X; heapify(arr, i, 0); } } void printArray(int arr[], int n) { for (int i=0; i<n; ++i) printf(“%d”,arr[i]); printf(“\n”); } int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); printf(“Sorted array is \n"); printArray(arr, n); }
a) swap(arr[0], arr[n])
b) swap(arr[i], arr[n])
c) swap(arr[0], arr[i])
d) swap(arr[i], arr[2*i])
View Answer
Explanation: Steps in heap sort are : (i) Build the max-heap, (ii) Swap the root element with the last element of the heap, (iii) Reduce the size of heap by 1 and heapify the root element, (iv) Repeat the steps form step number (v) until all the elements are sorted. Therefore the correct option is swap(arr[0], arr[i]).
8. Which one of the following is a variation of Heap sort?
a) Comb sort
b) Smooth sort
c) Binary tree sort
d) Shell sort
View Answer
Explanation: Smooth sort is a variation of Heap sort. Smooth sort has O(nlogn) worst case time complexity like Heap sort. But Smooth sort takes O(n) time to sort the nearly sorted input array.
9. Introsort algorithm is combination of _____________
a) Quick sort and Heap sort
b) Quick sort and Shell sort
c) Heap sort and Merge sort
d) Heap sort and insertion sort
View Answer
Explanation: Introsort is a hybrid sorting algorithm that combines Quick sort and Heap sort to retain advantages of both. It has worst case speed of Heap sort and average case speed of Quick sort.
10. How many elements can be sorted in O(logn) time using Heap sort?
a) O(1)
b) O(n/2)
c) O(logn/log(logn))
d) O(logn)
View Answer
Explanation: The time complexity of Heap sort is O(klogk) for k input elements,
for k = logn/log(logn),
O(klogk) = O(logn/log(logn) * log(logn/log(logn)))
∴ O(klogk) = O(logn/log(logn) * (log(logn) – log(log(logn))))
= O(logn)
Hence the correct option is O(logn/log(logn)).
Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.
To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Design and Analysis of Algorithms Books
- Apply for Computer Science Internship
- Practice Data Structure MCQ
- Practice Programming MCQs
- Practice Computer Science MCQs
