Independent Set Problem Questions and Answers

This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Independent Set Problem”.

1. Which of the following refers to the set of non-adjacent vertices?
a) Independent set
b) Dominant set
c) Vertex cover set
d) Edge cover set
View Answer

Answer: a
Explanation: In a graph G with V vertices and E edges, there exists a set of vertices, in which no two vertices are adjacent. This set of non-adjacent vertices is called an independent set i.e. no two vertices share a common edge.

2. Which of the following refers to the independence number of a graph?
a) Smallest size of a maximal independent set
b) Largest size of a minimal independent set
c) Smallest size of a minimal independent set
d) Largest size of a maximal independent set
View Answer

Answer: d
Explanation: In a graph G=(V, E) a subset S is an independent set if no two vertices in the S are adjacent. The independence number of graph G is the cardinality of the largest size of an independent set of vertices.

3. Given below is the pseudocode of the independent set problem. Which of the following best suits the blank?

Independent (G = (V, E))
{
    temp=true
    for every {u, v} in the subset
    {
        check if they have any edge between them
        if edge exist, then set ________________
    }
    If temp is true   
    correct result        
    else 
incorrect
}

a) temp to true and continue
b) temp to true and break
c) temp to false and break
d) temp to false and continue
View Answer

Answer: c
Explanation: The given pseudocode is for solving the independent set problem. First, initialize a temporary variable as true. Now, check that each pair of vertices belong to the set are adjacent or not, by checking if there exists any edge between them.

Sanfoundry Certification Contest of the Month is Live. 100+ Subjects. Participate Now!

4. What is the maximal independent set for the graph given below?

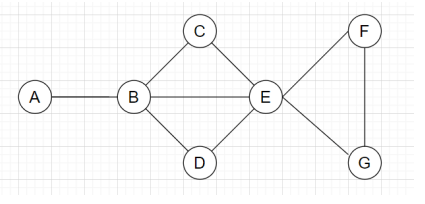
a) {C, D, E, G}
b) {A, C, D, F}
c) {A, E, B, C}
d) {A, B, C, D}
View Answer

Answer: b
Explanation: The maximal independent set S of a graph G contains the set of vertices, such that no two vertices should be adjacent and no vertex can be further added to the set. If we start with vertex A, we can’t select vertex B. Select vertex C and D, hence we can’t select E. Now, select any vertex from F and G according to the given options. Hence, the set contains the vertex {A, C, D, F}.

5. In a graph, an independent set is maximal if no further vertex can be added to the stay independent.
a) True
b) False
View Answer

Answer: a
Explanation: In a given graph G=(V, E), an independent set of G is a subset S of the vertices present in the graph G, such that no two vertices of S are adjacent in G. Hence, a maximal independent set of graph G is a set where it is impossible to add another vertex and stay independent.

6. What is the independence number of the graph given below?

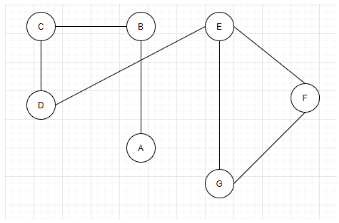
a) 1
b) 2
c) 3
d) 4
View Answer

Answer: c
Explanation: The independence number of the graph is given by the largest size of an independent set. If we start with vertex A, we can’t select vertex B. Select vertex C and vertex E. The maximal independent set of the graph will be {A, C, E}. Hence, the independence number of the graph is 3.

7. What is the size of the smallest maximal independent set of a chain of 7 nodes?
a) 1
b) 2
c) 3
d) 4
View Answer

Answer: c
Explanation: In a graph G, a set of vertices is an independent set if there is no common edge between them. A maximal independent set of graph G is a set where it is impossible to add another vertex to make it independent. Here, we can select the 2^nd, 5^th and 7^th node to get the smallest maximal independent set (1—2—3—4—5—6—7). Hence, the size of smallest maximal independent set of a chain of 7 nodes is 3.

8. The pseudocode for the independent set problem is given below. Which of the following gives the time complexity for it?

Independent (G = (V, E))
{
    temp=true
    for every {u, v} in the subset
    {
        check if they have any edge between them
        if edge exists, then set temp as false and break
    }
    If temp is true 
    correct result        
    else 
incorrect
}

a) O(V + E)
b) O(V)
c) O(V log V)
d) O(V log E)
View Answer

Answer: a
Explanation: To check whether the given subset of vertices of a given graph is an independent set, we need to check that all the vertices present in the set are non-adjacent. This can be done by confirming that they don’t share any edge. This can be performed in polynomial time. Hence, the time complexity is O(V + E).

Sanfoundry Global Education & Learning Series – Data Structures & Algorithms.

To practice all areas of Data Structures & Algorithms, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Vertex Cover Problem Multiple Choice Questions and Answers (MCQs)

» Next - Dominating Set Problem Multiple Choice Questions and Answers (MCQs)

Related Posts:

Recommended Articles: