This set of Strength of Materials Multiple Choice Questions & Answers (MCQs) focuses on “Bending Equation”.
1. In simple bending, ______ is constant.
a) Shear force
b) Loading
c) Deformation
d) Bending moment
View Answer
Explanation: If a beam is undergone with simple bending, the beam deforms under the action of bending moment. If this bending moment is constant and does not affect by any shear force, then the beam is in state of simple bending.
2. If a beam is subjected to pure bending, then the deformation of the beam is_____
a) Arc of circle
b) Triangular
c) Trapezoidal
d) Rectangular
View Answer
Explanation: The beam being subjected to pure bending, there will be only bending moment and no shear force it results in the formation of an arc of circle with some radius known as radius of curvature.
3. When a beam is subjected to simple bending, ____________ is the same in both tension and compression for the material.
a) Modulus of rigidity
b) Modulus of elasticity
c) Poisson’s ratio
d) Modulus of section
View Answer
Explanation: It is one of the most important assumptions made in the theory of simple bending that is the modulus of elasticity that is Young’s modulus [E] is same in both tension and compression for the material and the stress in a beam do not exceed the elastic limit.
4. E/R = M/I = f/y is a bending equation.
a) True
b) False
View Answer
Explanation: The above-mentioned equation is absolutely correct.
E/R = M/I = f/y is a bending equation. It is also known as flexure equation (or) equation for theory of simple bending.
Where,
E stands for Young’s modulus or modulus of elasticity.
R stands for radius of curvature.
M stands for bending moment
I stand for moment of inertia
f stands for bending stress
y stands for neutral axis.
5. Maximum Shearing stress in a beam is at _____
a) Neutral axis
b) Extreme fibres
c) Mid span
d) Action of loading
View Answer
Explanation: Shearing stress is defined as the resistance offered by the internal stress to the shear force. Shearing stress in a beam is maximum at a neutral axis.
6. At the neutral axis, bending stress is _____
a) Minimum
b) Maximum
c) Zero
d) Constant
View Answer
Explanation: Neutral axis is defined as a line of intersection of neutral plane or neutral layer on a cross section at the neutral axis of that section. At the NA, bending stress or bending strain is zero. The first moment of area of a beam section about neutral axis is also zero. The layer of neutral axis neither contracts nor extends.
7. Curvature of the beam is __________ to bending moment.
a) Equal
b) Directly proportion
c) Inversely proportion
d) Coincides
View Answer
Explanation: From the flexural equation, we have 1/R is called as the “curvature of the beam”.
1 / R = M / EI
Hence the curvature of the beam is directly proportional to bending moment and inversely proportional to flexural rigidity (EI).
8. What are the units of flexural rigidity?
a) Nm2
b) Nm
c) N/m
d) m/N3
View Answer
Explanation: The product of young’s modulus (E) of the material and moment of inertia (I) of the beam section about its neutral axis is called flexural rigidity.
Units for E are N/m2
Units for I are m4
Their product is Nm2.
9. What are the units for section modulus?
a) m2
b) m4
c) m3
d) m
View Answer
Explanation: The ratio of moment of inertia to the distance to the extreme fibre is called modulus of section or section modulus. It is generally denoted by the letter Z. Section modulus is expressed in m3
Z = I/y
= m4/ m
= m3.
10. What are the units of axial stiffness?
a) m3
b) m2
c) N/ m
d) -m
View Answer
Explanation: Axial rigidity is a product of young’s modulus (E) and the cross-sectional area (A) of that section. Axial rigidity per unit length is known as axial stiffness the si units of axial stiffness are Newton per metre (N/m).
11. Calculate the modulus of section of rectangle beam of size 240 mm × 400 mm.
a) 5.4 × 106 mm3
b) 6.2 × 106 mm3
c) 5.5 × 106 mm3
d) 6.4 × 106 mm3
View Answer
Explanation: b = 240 mm & d = 400 mm
Moment of inertia (I) = bd3/12; y = d/2
Section modulus (Z) = I/y = bd2/ 6
= 1/6 × 240 × 400 ×400
= 6.4 × 106 mm3.
12. What is the product of force and radius?
a) Twisting shear
b) Turning shear
c) Turning moment
d) Tilting moment
View Answer
Explanation: Twisting moment will be equal to the product of the perpendicular force and existing radius. Denoted by letter T and SI units are Nm.
13. Determine section modulus for beam of 100mm diameter.
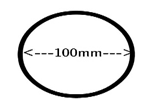
a) 785 × 103 mm3
b) 456 × 103 mm3
c) 87 × 103 mm3
d) 98 × 103 mm3
View Answer
Explanation: d = 300mm
For circular sections; I = π / 64 × d4
y= d/2
Z = π/32 × d3 (d = 100 mm)
Z = 98.17 × 103mm3.
Sanfoundry Global Education & Learning Series – Strength of Materials.
To practice all areas of Strength of Materials, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Metallurgical Engineering MCQs
- Apply for Mechanical Engineering Internship
- Check Metallurgical Engineering Books
- Check Mechanical Engineering Books
- Check Strength of Materials Books
