This set of Strength of Materials Multiple Choice Questions & Answers (MCQs) focuses on “Pure Bending Stress”.
1. In simply supported beams, the _____ stress distribution is not uniform.
a) Bending
b) Shearing
c) Tensile
d) Compressive
View Answer
Explanation: In a simply supported beam, there is compressive stress above the neutral axis and tensile stress below it. It bends with concavity upwards. Hence the bending stress distribution is not uniform over the section.
2. The maximum _________ stresses occur at top most fibre of a simply supported beam.
a) Tensile
b) Compressive
c) Shear
d) Bending
View Answer
Explanation: As bending stress distribution is not uniform over the section in simply supported beams, the maximum compressive stress lies above the neutral axis. Obviously, top most fibre of beam. The maximum tensile stress occurs at bottom most fibre.
3. The stress is directly proportional to _______
a) E
b) u
c) y
d) R
View Answer
Explanation: By two equations; we have e = y/R & e = f/E
Equating both equations; we get e = f/E = y/R
Hence stress (f) is directly proportional to the distance from neutral axis(y).
4. At the extreme fibre, bending stress is______
a) Minimum
b) Zero
c) Constant
d) Maximum
View Answer
Explanation: Bending stress is defined as the resistance offered by internal stress to bending. In beams, stresses occurs above or below the neutral axis i.e at the extreme fibres. Hence bending stress is maximum at the extreme fibres.
5. The curvature of a beam is equal to _____
a) EI/M
b) M/E
c) M/EI
d) E/MI
View Answer
Explanation: From the bending equation, E/R = M/I = f/y.
Where R is called “radius of curvature “
1/R is called “curvature of the beam “.
So, 1/R = M/EI.
So curvature of the beam is directly proportional to bending moment.
6. Skin stress is also called as ______
a) Shear stress
b) Bending stress
c) Lateral stress
d) Temperature stress
View Answer
Explanation: The bending moment leads to deform or deflect the beam and internal stress resists bending. The resistance offered by internal stress to bending is called bending stress or “fibre stress” or “skin stress” or “longitudinal stress”.
7. _________ is the total Strain energy stored in a body.
a) modulus of resilience
b) impact energy
c) resilience
d) proof resilience
View Answer
Explanation: When a load acts on a body, there is deformation of the body which causes movement of the applied load. Thus work is done is stored in the body as energy and the load is removed this stored energy which is by virtue of strain is called resilience.
8. In cantilever beams, there is _______ stress above neutral axis.
a) Compressive
b) Tensile
c) Temperature
d) Shear
View Answer
Explanation: In a cantilever beam maximum compressive stress occurs at bottom most fibre and maximum tensile stress occurs at the top most fibre and zero at neutral axis hence the tensile stresses lies above the neutral axis.
9. The product of modulus of elasticity (E) and polar moment of inertia (J) is called torsional rigidity.
a) True
b) False
View Answer
Explanation: The product of the modulus of rigidity (C) and polar moment of inertia (J) is called torsional rigidity and it produces a twist of one radian in a shaft of unit length.
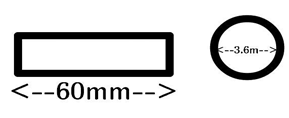
10. Calculate the maximum stress due to Bending in a steel strip of 30 mm thick and 60 mm wide is bent around a circular drum of 3.6 m diameter [Take Young’s modulus = 200kN/m2].
a) 2341.76 N/mm2
b) 1666.67 N/mm2
c) 5411.76 N/mm2
d) 4666.67 N/mm2
View Answer
Explanation: Thickness of steel strip = 30 mm; b = 60 mm; d = 3.6m
R = 3.6/2 = 1.8 m
E = 200 kN/m2
y = 30/2 = 15 mm
E/R = f/y ; f = 200000×15/1800
= 1666.67 N/mm2.
11. The strength of beams depend merely on________
a) Modulus section
b) Moment of inertia
c) Flexural rigidity
d) Moment of resistance
View Answer
Explanation: The ratio of moment of inertia to the distance to the extreme fibre is called modulus of section. The Beam is stronger when section modulus is more. The strength of beam depends on section modulus. The beams of same strength mean section modulus is same for the beams.
12. The steel plate is bent into a circular path of radius 10 metres. If the plate section be 120 mm wide and 20 mm thick, then calculate the maximum bending stress. [Consider Young’s modulus = 200000 N/mm2].
a) 350 N/mm2
b) 400 N/mm2
c) 200 N/mm2
d) 500 N/mm2
View Answer
Explanation: R = 10000 mm; y = 20/2 = 10 mm; E = 200000 N/mm2
By bending equation we have E/R = f/y
f = 200000×10 / 10000
= 200 N/mm2.
Sanfoundry Global Education & Learning Series – Strength of Materials.
To practice all areas of Strength of Materials, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Metallurgical Engineering Books
- Practice Metallurgical Engineering MCQs
- Check Strength of Materials Books
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
