This set of Strength of Materials Interview Questions and Answers for freshers focuses on “Bars of Composite Sections – 2”.
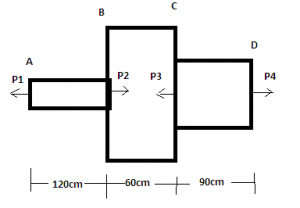
1. A member ABCD is subjected to points load P1=45kN, P2, P3=450kN and P4=130kN. what will be the value of P necessary for equilibrium?
a) 350kN
b) 365kN
c) 375kN
d) 400kN
View Answer
Explanation: On resolving forces P1 + P3 = P2 + P4
So P2 = 45 + 450 – 130 I.e. P2 = 365kN.
2. A member ABCD is subjected to points load P1=45kN, P2, P3=450kN and P4=130kN. What will be the total elongation of the member, assuming the modulus of elasticity to be 2.1x105N/mm2. The cross sectional area is 625mm, 2500mm, 1250mm respectively.
a) 0.4914mm
b) 0.4235mm
c) 0.4621mm
d) 0.4354mm
View Answer
Explanation: First of all the fores will be calculated
on resolving forces P1 + P3 = P2 + P4
So P2 = 45 + 450 – 130 I.e. P2 = 365kN
So forces on three sections will be 45kN, 320kN and 130kN respectively.
After that increase in length = PL/AE for all three sections will be calculated.
3. A tensile rod of 40kN is acting on a rod of diameter 40mm and of length 4m. a bore of diameter 20mm is made centrally on the rod. To what length the rod should be bored so that the total extension will increase 30% under the same tensile load if E = 2×105 N/mm2?
a) 2m
b) 2.7m
c) 3.2m
d) 3.6m
View Answer
Explanation: The extension = PL / AE = 2/π mm
Extension after the bore is made = 1.3x 2/π mm = 2.6/π mm
The extension after the bore is made, is also obtained by finding the extension of the un bored length and bored length.
Stress = load / area
So total extension after bore is made can have two equations which can be put equal and the length the rod should be bored up is calculated.
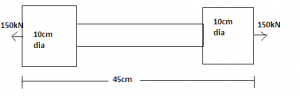
4. A bar is subjected to a tensile load of 150kN. If the stress in the middle portion is limited to 160 N/mm2, what will be the diameter of the middle portion of the total elongation of the bar is 0.25cm (E= 2 x 105)?
a) 3cm
b) 3.45cm
c) 3.85cm
d) 4cm
View Answer
Explanation: Total extension = P/E x (L1/A1 + L2/A2 + L3/A3 )
Only variable in the equation is A2. after getting this the diameter of the section can be calculated.
5. A rod, which tapers uniformly from 5cm diameter to 3cm diameter in a length of 50cm, is subjected to an axial load of 6000N. if E = 2,00,000 N/mm2, what will be the extension of the rod?
a) 0.00114cm
b) 0.00124cm
c) 0.00127cm
d) 0.00154cm
View Answer
Explanation: The extension in the rod = PL / Et(a-b) x loge (a/b)
Where a = 50mm, b = 30mm.
6. A bar is in two sections having equal lengths. The area of cross section of 1st is double that of 2nd. if the bar carries an axial load of P, then what will be the ratio of elongation in section 2nd to section 1st ?
a) 1/2
b) 2
c) 4
d) 1/4
View Answer
Explanation: Ratio of elongation in 2nd / ratio of elongation in 1st = L2/L1 x A2/A1
Since L1 = L2 and A1 = 2A2
Therefore, ratio = 1 x 2/1 = 2.
7. A round bar made of same material consists of 4 parts each of 100mm length having diameters of 40mm, 50mm, 60mm and 70mm, respectively. If the bar is subjected to an axial load of 10kN, what will be the total elongation of the bar in mm?
a) 0.4/πE ( 1/16 + 1/25 + 1/36 + 1/49)
b) 4/πE ( 1/16 + 1/25 + 1/36 + 1/49)
c) 2/πE ( 1/16 + 1/25 + 1/36 + 1/49)
d) 40/πE ( 1/16 + 1/25 + 1/36 + 1/49)
View Answer
Explanation: Total elongation = 4PL/πE ( 1/d12 + 1/d22 + 1/d32 + 1/d42)
= 4x10x100/πEx100 ( 1/16 + 1/25 + 1/36 + 1/49) mm
= 40/πE ( 1/16 + 1/25 + 1/36 + 1/49).
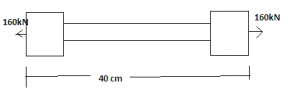
8. A bar shown in the diagram below is subjected to load 160kN. If the stress in the middle portion Is limited to 150N/mm2, what will be the length of the middle portion, if the total elongation of the bar is to be 0.2mm? Take E = 2.1 x 105 N/mm2.
a) 18.45cm
b) 17.24cm
c) 16.45cm
d) 20.71cm
View Answer
Explanation: Let L2 and D2 be the dimensions of the middle portion and L1 and D2 be the end portion dimensions.
For middle portion area = load / stress
This gives area by which diameter can be calculated.
As Total extension = P/E x (L1/A1 + L2/A2)
This gives the value of L2.
9. A composite bar consists of a bar enclosed inside a tune of another material when compressed under a load as whole through rigid collars at the end of the bar. What will be the equation of compatibility?
a) W1 + W2 = W
b) W1 + W2 = constant
c) W1/A1E1 = W2/A2E2
d) W1/A1E2 = W2/A2E1
View Answer
Explanation: Compatibility equation insists that the change in length of the bar must be compatible with the boundary conditions. Here W1 + W2 = W it is also correct but it is equilibrium equation.
Sanfoundry Global Education & Learning Series – Strength of Materials.
To practice all areas of Strength of Materials for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Metallurgical Engineering Books
- Apply for Metallurgical Engineering Internship
- Check Mechanical Engineering Books
- Practice Metallurgical Engineering MCQs
- Check Strength of Materials Books
