This set of Engineering Hydrology Multiple Choice Questions & Answers (MCQs) focuses on “Mean Precipitation Over an Area”.
1. Which is not a method of finding out the average value of precipitation from the rainfall data of different stations?
a) Thiessen polygon method
b) Arithmetical mean method
c) Geometric mean method
d) Isohyetal method
View Answer
Explanation: The point rainfall data of different stations are collected. Then the average value of precipitation is being calculated. There are three methods that are used to calculate mean precipitation. They include (1) Thiessen polygon method (2) Arithmetical mean method and (3) Isohyetal method. The Geometric mean method is not used to calculate average precipitation but it is one of the methods of population forecasting.
2. What is an Isohyet?
a) The line joining the points of equal amount of snow
b) The line joining the points of equal atmospheric pressure
c) The line joining the points of equal elevation
d) The line joining the points of equal rainfall
View Answer
Explanation: The line joining the points of equal rainfall is called an isohyet. The line joining the points of equal amount of snow is called an isomif. The line joining the points of equal atmospheric pressure is called an isobar. The line joining the points of equal elevation is called a contour line.
3. The formula of the Arithmetical mean method for calculating the average precipitation on the basis of rainfall data of five stations?
Note – Symbols have their usual meanings.
a) (P1 + P2 + P3 + P4 + P5) / 5
b) (P1 + P2 + P3 + P4 + P5) / (P1 * P2 * P3 * P4 * P5)
c) 5 / ((1 / P1) + (1 / P2) + (1 / P3) + (1 / P4) + (1 / P5))
d) (P1 * P2 * P3 * P4 * P5) / (P1 + P2 + P3 + P4 + P5)
View Answer
Explanation: The point rainfall data of different rain gauge stations are collected. Then the average precipitation is calculated by different methods. The arithmetical mean method is one of the methods. Its formula is as follows-
Mean Precipitation = (P1 + P2 + P3 + P4 + P5) / 5
4. What is the formula for finding out average precipitation by Theissen polygon method?
Note – A1, A2, A3, A4 are areas of surrounding the rain gauge stations and P1, P2, P3, P4 are precipitation values recorded in those stations respectively.
a) (P1 + P2 + P3 + P4) / 4
b) (P1 * A1 + P2 * A2 + P3 * A3 + P4 * A4) / (A1 + A2 + A3 + A4)
c) (P1 * A1 + P2 * A2 + P3 * A3 + P4 * A4) / (A1 * A2 * A3 * A4)
d) 100 / ((A1 / P1) + (A2 / P2) + (A3 / P3) + (A4 / P4))
View Answer
Explanation: In the Theissen polygon method the rainfall data collected firstly. Then the area enclosing the station is marked. Like this, the whole catchment is divided into small areas by a network of triangles. Then the mean precipitation is calculated by the following formula-
Mean Precipitation = (P1 * A1 + P2 * A2 + P3 * A3 + P4 * A4) / (A1 + A2 + A3 + A4)
5. What is the formula used in the Isohyetal method for finding out mean precipitation?
Note – A1, A2, A3, A4 are areas of surrounding the rain gauge stations and P1, P2, P3, P4, P5 are precipitation values recorded in those stations respectively.
a) (A1 * (P1 + P2) / 2 + A2 * (P2 + P3) / 2 + A3 * (P3 + P4) / 2 + A4 * (P4 + P5) / 2) / (A1 + A2 + A3 + A4)
b) (P1 * A1 + P2 * A2 + P3 * A3 + P4 * A4) / (A1 + A2 + A3 + A4)
c) (A1 * (P1 + P2) / 2 + A2 * (P2 + P3) / 2 + A3 * (P3 + P4) / 2 + A4 * (P4 + P5) / 2) / (A1 * A2 * A3 * A4)
d) (P1 * A1 + P2 * A2 + P3 * A3 + P4 * A4) / (A1 * A2 * A3 * A4)
View Answer
Explanation: Isohyet is the line joining points of equal rainfall. In the Isohyetal method, the catchment area is divided into small areas. The formula for calculating average precipitation by this method is as follows-
Mean precipitation = (A1 * (P1 + P2) / 2 + A2 * (P2 + P3) / 2 + A3 * (P3 + P4) / 2 + A4 * (P4 + P5) / 2) / (A1 + A2 + A3 + A4)
6. The ratio Ai / A is known as ____________ (where ‘Ai’ is the area of the ith zone of the catchment and ‘A’ is the total area of the catchment)
a) Area factor
b) Weightage factor
c) Area index
d) Weight index
View Answer
Explanation: In the Theissen polygon method, the rainfall data of various stations are collected for a catchment area. The weighted average of the precipitation is calculated. The factor Ai / A is known as the weightage factor.
7. Which of the following statement is correct regarding the calculation of the value of average precipitation by Theissen polygon method and Arithmetical mean method for the same catchment area?
a) Theissen polygon method = Arithmetical mean method
b) Theissen polygon method < Arithmetical mean method
c) Theissen polygon method > Arithmetical mean method
d) Theissen polygon method ≤ Arithmetical mean method
View Answer
Explanation: The value of average precipitation is more in the case of the Theissen polygon method as compared to the Arithmetical mean method. This is because more weightage is given to some stations. Also, the stations outside the catchment area are used effectively in the case of the Theissen polygon method.
8. The rainfall data recorded at different rain gauge stations in a catchment area are 3cm, 6cm, 6.5cm, 7cm and 10cm. Calculate the average depth of rainfall by the Arithmetic Mean Method.
a) 7 cm
b) 6.5 cm
c) 6 cm
d) 7.5 cm
View Answer
Explanation: The rainfall data are as follows: –
P1 = 3 cm
P2 = 6 cm
P3 = 6.5 cm
P4 = 7 cm
P5 = 10 cm
Average depth of rainfall = (P1 + P2 + P3 + P4 + P5) / 5
= {(3 + 6 + 6.5 + 7 + 10) / 5} cm
= 6.5 cm
9. Calculate the mean precipitation by the Isohyetal method. The rainfall data of various stations are given below-
| Isohyets(cm) | 22-18 | 18-14 | 14-10 | 10-6 |
| Area of catchment(km2) | 34 | 120 | 60 | 45 |
a) 13 cm
b) 13.5 cm
c) 14.2 cm
d) 14.8 cm
View Answer
Explanation: Rainfall data, P1 = 22 cm
P2 = 18 cm
P3 = 14 cm
P4 = 10 cm
P5 = 6 cm
Area of catchment, A1 = 34 km2
A2 = 120 km2
A3 = 60 km2
A4 = 45 km2
By Isohyetal method,
Mean precipitation = (A1 * (P1 + P2) / 2 + A2 * (P2 + P3) / 2 + A3 * (P3 + P4) / 2 + A4 * (P4 + P5) / 2) / (A1 + A2 + A3 + A4)
= (34 * (22 + 18) / 2 + 120 * (18 + 14) / 2 + 60 * (14 + 10) / 2 + 45 * (10 + 6) / 2) / (34 + 120 + 60 + 45) cm
= 14.21 cm
10. The Theissen polygon areas of four rain gauging stations and the rainfall data recorded in each station is as follows-
| Rainfall (cm) | 6 | 10 | 8 | 13 |
| Areas within the catchment (km2) | 70 | 123 | 155 | 160 |
Calculate the average depth of Rainfall in cm.
a) 7.98 cm
b) 8.5 cm
c) 8.78cm
d) 9.78 cm
View Answer
Explanation: The rainfall data are as follows: –
P1 = 6 cm
P2 = 10 cm
P3 = 8 cm
P4 = 13 cm
Theissen polygon areas are as follows: –
A1 = 70 km2
A2 = 123 km2
A3 = 155 km2
A4 = 160 km2
By Theissen polygon method,
Mean Precipitation = (P1 * A1 + P2 * A2 + P3 * A3 + P4 * A4) / (A1 + A2 + A3 + A4)
= (6 * 70 + 10 * 123 + 8 * 155 + 13 * 160) / (70 + 123 + 155 + 160) cm
= 9.78 cm
11. The rainfall data recorded at rain gauge stations 1, 2, 3, 4 & 5 are 11cm, 15cm, 16cm, 20cm & 24cm respectively. If the Theissen weightage factors are 0.24, 0.16, 0.33, 0.22 & 0.28 respectively then find the average depth of precipitation.
a) 20 cm
b) 21.44 cm
c) 23.45 cm
d) 18.56 cm
View Answer
Explanation: The rainfall data are as follows: –
P1 = 11 cm
P2 = 15 cm
P3 = 16 cm
P4 = 20 cm
P5 = 24 cm
Weightage factors are
A1 / A = 0.24
A2 / A = 0.16
A3 / A = 0.33
A4 / A = 0.22
A5 / A = 0.28
By Theissen polygon method,
Average depth of rainfall = ((P1 * A1 / A) + (P2 * A2 / A) + (P3 * A3 / A) + (P4 * A4 / A) + (P5 * A5 / A))
= ((11 * 0.24) + (15 * 0.16) + (16 * 0.33) + (20 * 0.22) + (24 * 0.28)) cm
= 21.44 cm
12. Calculate the mean precipitation by the Isohyetal method. The rainfall data of various stations are given below-
| Isohyets(cm) | 14 | 14-12 | 12-10 | 10-8 |
| Area of catchment(km2) | 30 | 120 | 84 | 50 |
a) 12.9 cm
b) 15.5 cm
c) 16.2 cm
d) 11.8 cm
View Answer
Explanation: Rainfall data, P1 = 14 cm
P2 = 12 cm
P3 = 10 cm
P4 = 8 cm
Area of catchment, A1 = 30 km2
A2 = 120 km2
A3 = 84 km2
A4 = 50 km2
By Isohyetal method,
Mean precipitation = (A1 * P1 + A2 * (P1 + P2) / 2 + A3 * (P2 + P3) / 2 + A4 * (P3 + P4) / 2) / (A1 + A2 + A3 + A4)
= (30 * 14 + 120 * (14 + 12) / 2 + 84 * (12 + 10) / 2 + 50 * (10 + 8) / 2) / (30 + 120 + 84 + 50) cm
= 11.81 cm
13. The figure given below shows a catchment area which consists of an equilateral triangle with each side being 4 km and a square having each side as 4 km. The rain gauging stations are marked by red dots and the rainfall data at each station is written beside it. Find the mean precipitation by Theissen polygon method.
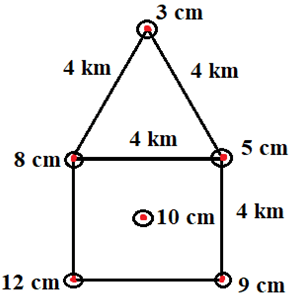
a) 7.02 cm
b) 8.06 cm
c) 8.98cm
d) 9.78 cm
View Answer
Explanation: The rainfall data are as follows: –
P1 = 3 cm
P2 = 8 cm
P3 = 5 cm
P4 = 9 cm
P5 = 12 cm
P6 = 10 cm
In the figure,
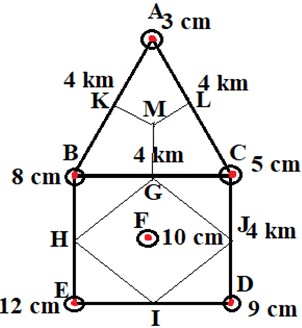
Draw the perpendicular bisectors KM, MG and ML of side AB, BC and CA respectively.
Divide the square into 4 corner triangles which are the effective areas of the four corner stations B, C, E and D respectively.
Now, GH = GJ = JI = IH
Calculation of effective areas of different stations,
For station A, Effective area (A1) = (1 / 3) * Area of triangle ABC
= (1 / 3) * (0.5 * BC * AG)
= (1 / 3) * (0.5 * 4 * (√(AB2 – BG2)))
= (1 / 3) * (0.5 * 4 * (√(42 – 22))) km2
= 4 / √3 = 2.309 km2
Area of BHG = Area of GCJ = Area of JDI = Area of HEI = 0.5 * 2 * 2 = 2 km2
Area of GHIJ = Area of square BCDE – 4 * Area of BHG
= (4 * 4) – (4 * 2) km2
= (16 – 8) km2
= 8 km2
For station B, Effective area (A2) = (1 / 3) * Area of triangle ABC + Area of BHG
= (2.309 + 2) km2 = 4.309 km2
For station C, Effective area (A3) = (1 / 3) * Area of triangle ABC + Area of GCJ
= 4.309 km2
For station D, Effective area (A4) = Area of JDI
= 2 km2
For station E, Effective area (A5) = Area of HEI
= 2 km2
For station F, Effective area (A6) = Area of GHIJ = 8 km2
By Theissen polygon method,
Mean Precipitation = (P1 * A1 + P2 * A2 + P3 * A3 + P4 * A4 + P5 * A5 + P6 * A6) / (A1 + A2 + A3 + A4 + A5 + A6)
= (3 * 2.309 + 8 * 4.309 + 5 * 4.309 + 9 * 2 + 12 * 2 + 10 * 8) / (2.309 + 4.309 + 4.309 + 2 + 2 + 8)
= 8.06 cm
Sanfoundry Global Education & Learning Series – Engineering Hydrology.
To practice all areas of Engineering Hydrology, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
