This set of Engineering Hydrology Multiple Choice Questions & Answers (MCQs) focuses on “Synthetic Unit Hydrograph – Set 2”.
1. Two square catchments A and B having same topographical features but of different size are present next to each other with their sides parallel. A long straight water stream passes through both the catchments intercepting the centroids of both A and B. The side length of B is 3 times that of A. Let tA and tB be the lag times for A and B, respectively. If tA and tB are related to each other as per Snyder equation as tA = K.tB, what is the value of K?
a) 0.52
b) 0.81
c) 1.57
d) 1.93
View Answer
Explanation: Let the side length of catchment A be ‘a’.
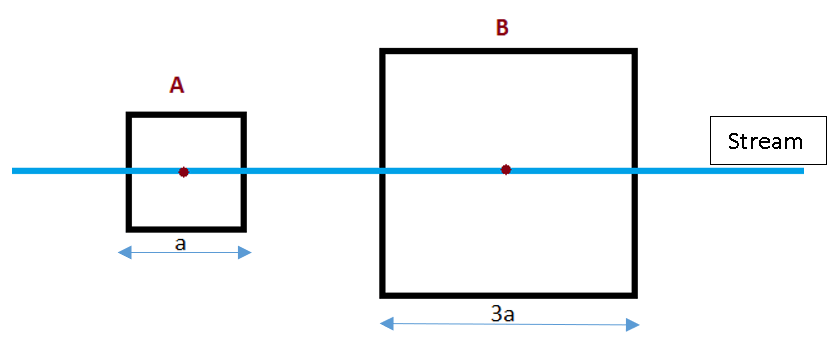
So, \(\frac{t_A}{t_B} = \frac{[C_t.(a.\frac{a}{2})^{0.3}]}{[C_t.(3a.\frac{3a}{2})^{0.3}]} \)
→ \(\frac{t_A}{t_B} = \frac{(\frac{1}{2})^{0.3}}{\frac{9}{2})^{0.3}} = \frac{0.8122}{1.5702}\)=0.5173 ≅ 0.52
∴ tA=0.52*tB
2. The basin lag for a drainage area is given by,
t=Ct.\((\frac{LL_{ca}}{\sqrt{s}})^{0.38} \)
where, t is in hours, lengths are in km and S is the basin slope. If the slope of the basin is reduced by 50%, then what will be the corresponding change in basin lag?
a) Increases by 14%
b) Increases by 25%
c) Decreases by 14%
d) Decreases by 25%
View Answer
Explanation: As per the given equation, the basin lag varies with the slope as,
t∝\((\frac{1}{\sqrt{S}})^{0.38}\) ⇒ t∝S-0.19
Let the new basin lag be ‘t1’ and the new slope be ‘S1’. So,
\(\frac{t_1}{t}=\frac{S_1^{-0.19}}{S^{-0.19}}=\frac{(0.5*S)^{-0.19}}{(S)^{-0.19}}\) =(0.5)-0.19=1.1407
→ t1=1.1407*t≅1.14*t
Therefore, the basin lag time increases by 14%.
3. What is the ratio of standard duration of rainfall excess to the basin lag time for a given catchment as per Snyder?
a) 0.18
b) 0.81
c) 1.5
d) 5.5
View Answer
Explanation: Snyder developed an equation to find the standard duration ‘D’ hours of effective rainfall from the basin lag time. It is given as D=\(\frac{t}{5.5}\). So, \(\frac{D}{t}=\frac{1}{5.5}\)=0.18.
4. For an effective rainfall of 1 hour standard duration over a catchment of area 30000 hectares, what will be the peak discharge (in m3/s) of a 1 hour unit hydrograph? Assume Snyder’s regional constant as Cp = 0.66.
a) 10
b) 55
c) 100
d) 550
View Answer
Explanation: Given, D = 1 hour, A = 30000 ha = 300 km2, Cp = 0.66. So,
D=\(\frac{t}{5.5}\) ⇒ t=5.5*D=5.5*1=5.5 hours
∴ Qps=\(\frac{2.78*C_p*A}{t}=\frac{2.78*0.66*300}{5.5}\)=100.08 m3/s ≈ 100 m3/s
5. The lag time for a basin estimated by Snyder’s equation is 11 hours. An effective rainfall of 3 hours occurs on the basin. What is the value of basin lag (in minutes) used to derive a unit hydrograph for the basin?
a) 550
b) 600
c) 650
d) 675
View Answer
Explanation: The basin lag of 11 hours is used to derive unit hydrograph if the duration of effective rainfall is equal to the standard duration ‘D’.
D=\(\frac{t}{5.5}=\frac{11}{5.5}\) = 2 hours ≠ actual effective rainfall duration
Which implies that the initial basin lag value of 2 hours needs to be modified as per the actual rainfall.
Let the modified basin lag be tact and actual duration be Dact. So according to Snyder,
tact=t+\((\frac{D_{act}-D}{4})\)=11+\((\frac{3-2}{4})\)=11.25 hours=11.25*60 minutes=675 minutes
Thus, the new value of lag time tact must be used to calculate further data to derive the unit hydrograph.
6. A watershed has a lag time of 420 minutes. A storm of 60 minutes duration occurred over the area. A unit hydrograph is to be plotted by Snyder method. Which of the following is correct regarding the lag time used for calculating the peak discharge?
a) Equal to 420 minutes
b) Lesser than 420 minutes
c) More than 420 minutes
d) Cannot be determined
View Answer
Explanation: Given t = 420 minutes = 7 hours
D=\(\frac{t}{5.5}=\frac{7}{5.5}\)=1.273 hours
But Dact = 60 minutes = 1 hour. Which implies that the lag time needs to be modified.
∴ tact = t+\(\frac{(D_{act}-D}{4})\) = 7+\((\frac{1-1.273}{4})\)=6.93 hours≅416 minutes < 420 minutes
7. Which of the following quantities is commonly calculated for the plotting of a synthetic unit hydrograph?
a) Width of unit hydrograph at 25% of peak discharge
b) Width of unit hydrograph at 33% of peak discharge
c) Width of unit hydrograph at 50% of peak discharge
d) Width of unit hydrograph at 65% of peak discharge
View Answer
Explanation: To help in the plotting of unit hydrographs, the widths of unit hydrograph at 50% and 75% of peak discharge are commonly calculated from empirical equations correlating it to the peak discharge and area values.
8. For suitable application of Snyder’s method to develop unit hydrograph, it is required to have past data from meteorologically similar catchments.
a) True
b) False
View Answer
Explanation: The coefficients Ct and Cp used in the calculation of lag time and peak discharge respectively have largely varying values and hence it is advised that these values be calculated from past authentic unit hydrographs of similar catchments and then used for the catchment under study.
9. Which of the following quantities is required to calculate the unit hydrograph time base by Snyder’s method?
a) Basin lag
b) Peak discharge
c) Standard effective rainfall duration
d) Actual effective rainfall duration
View Answer
Explanation: The equation for calculating time base ‘tb’ of unit hydrograph given by Snyder is,
tb=(72+(3*tact)) hours
where, tact = actual basin lag.
10. Which of the following quantities needs to be changed first to improve the accuracy of the synthetic unit hydrograph?
a) Time base
b) Width of hydrograph at 50% peak discharge
c) Peak discharge
d) Basin lag
View Answer
Explanation: Out of all the parameters, the time base is the least accurate. After plotting the first iteration of the UH, it needs to be checked whether the area under the curve represents unit runoff volume. If not, the time base needs to be adjusted accordingly.
Sanfoundry Global Education & Learning Series – Engineering Hydrology.
To practice all areas of Engineering Hydrology, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
