This set of Engineering Hydrology Multiple Choice Questions & Answers (MCQs) focuses on “Hydrologic Channel Routing – Set 3”.
1. One set of inflow and outflow hydrograph is available for a reach. A plot between which of the following quantities is used to find the weighting factor ‘x’ for the reach? I = inflow, Q = outflow, t = time interval in hydrograph.
a) (I – Q) and [x.I + (1 – x).Q]
b) (I – Q).t and [x.I + (1 – x).Q]
c) (I – Q) and [x.I + (1 – x).Q].t
d) (I – Q).t and [x.I + (1 – x).Q].t
View Answer
Explanation: If one set of inflow of outflow hydrograph is given for a reach, the routing coefficients can be found by trial and error by assuming a value of x. The storage is calculated from the given values as the difference of inflow and outflow multiplied by the time interval. This quantity is plotted against the corresponding values of [x.I + (1 – x).Q] for a given set of inflow and outflow values.
2. The value of weighting factor for which the graph between storage and [x.I + (1 – x).Q] gives a straight line, is chosen as the weighting factor for that channel.
a) True
b) False
View Answer
Explanation: Plots between storage and the quantity [x.I + (1 – x).Q] are drawn for an assumed value of x by trial and error. The value of weighting factor which gives a straight line plot is chosen as the correct value for that reach.
3. A linear plot is obtained between storage and [x.I + (1 – x).Q] for a given weightage factor x. How is the storage-time constant for the reach found from the plot?
a) x- intercept of the line
b) y-intercept of the line
c) Slope of the line
d) Inverse slope of the line
View Answer
Explanation: On the x-axis, storage has dimensions of [L3] and on the y-axis the dimension of the quantity is [L3T]. The slope of the line will give a quantity with dimension [T-1]. Since the dimension of storage-time constant is that of time, inverse of the slope will give its value.
4. Find the storage-time constant of a channel from the graph shown below. The weighting factor is 0.3.
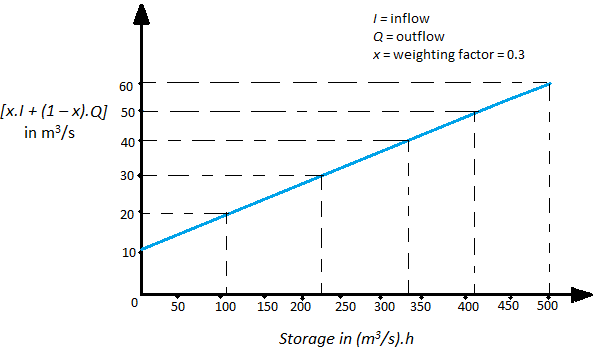
a) 6.4 hours
b) 9.2 hours
c) 11.8 hours
d) 13.7 hours
View Answer
Explanation: Choosing the ordinate values of 30 and 60 m3/s and the corresponding storage values,
Slope of line=\(\frac{(60-30) \frac{m^3}{s}}{(500-225) \frac{m^3}{s.h}}=\frac{30}{275}\)=0.1091 hour-1
∴Storage time constant,K=inverse of slope=\(\frac{275}{30}\)=9.1667≅9.2 hours
5. Which of the following represents the Muskingum routing equation to find the outflow at the end of time interval i to j? I is inflow, Q is outflow and C0, C1 and C2 are routing coefficients.
a) Qj=C0 Ij+C1 Ii+C2 Qi
b) Qj=C0 Qi+C1 Ij+C2 Ii
c) Qj=C0 Ii+C1 Qi+C2 Ij
d) Qj=C0 Qi+C1 Ii+C2 Ij
View Answer
Explanation: The Muskingum routing equation is derived by equating the storage difference from Muskingum equation to that from continuity equation. The equation of outflow at the end of an interval thus obtained is Q2=C0 I2+C1 I1+C2 Q1, where 1 and 2 represent start and end of the time interval.
6. Which of the following is not one of the Muskingum routing coefficients? K is the storage-time constant, x is the weighting factor and t is the time interval.
a) \(\frac{-Kx+0.5t}{K-Kx+0.5t}\)
b) \(\frac{Kx+0.5t}{K-Kx+0.5t}\)
c) \(\frac{-K+Kx-0.5t}{K-Kx+0.5t}\)
d) \(\frac{K-Kx-0.5t}{K-Kx+0.5t}\)
View Answer
Explanation: There are three coefficients in the Muskingum routing equation and they are given as,
C0=\(\frac{-Kx+0.5t}{K-Kx+0.5t}, C_1=\frac{Kx+0.5t}{K-Kx+0.5t} and C_2=\frac{K-Kx-0.5t}{K-Kx+0.5t}\)
7. What is the relationship between the Muskingum routing coefficients?
a) C1-C2=1-C0
b) C1-C2=1+C0
c) C1+C2=1-C0
d) C1+C2=1+C0
View Answer
Explanation: Using the formulae of the Muskingum routing coefficients,
C1-C2=\(\frac{Kx+0.5t}{K-Kx+0.5t}-\frac{K-Kx-0.5t}{K-Kx+0.5t}=\frac{Kx+0.5t-K+Kx+0.5t}{K-Kx+0.5t}=\frac{-K+2Kx+t}{K-Kx+0.5t}\)⋯⋯(1)
C1+C2=\(\frac{Kx+0.5t}{K-Kx+0.5t}+\frac{K-Kx-0.5t}{K-Kx+0.5t}=\frac{Kx+0.5t+K-Kx-0.5t}{K-Kx+0.5t}=\frac{K}{K-Kx+0.5t}\)⋯⋯(2)
1-C0=\(1-\frac{-Kx+0.5t}{K-Kx+0.5t}=\frac{K-Kx+0.5t+Kx-0.5t}{K-Kx+0.5t}=\frac{K}{K-Kx+0.5t}\)⋯⋯(3)
1+C0=\(1+\frac{-Kx+0.5t}{K-Kx+0.5t}=\frac{K-Kx+0.5t-Kx+0.5t}{K-Kx+0.5t}=\frac{K-2Kx+t}{K-Kx+0.5t}\)⋯⋯(4)
Comparing (1), (2), (3) and (4), we see that (2) = (3).
Therefore, C1+C2=1-C0 or C0+C1+C2=1
8. For a channel with a storage-time constant of 11.5 hours and weighting factor of 0.15, find the value of the first Muskingum routing coefficient (C0). Take time interval as 4 hours.
a) 0.023
b) 0.032
c) 0.035
d) 0.053
View Answer
Explanation: The first routing coefficient is given as,
C0=\(\frac{-Kx+0.5t}{K-Kx+0.5t}=\frac{(-11.5*0.15)+(0.5*4)}{11.5-(11.5*0.15)+(0.5*4)}=\frac{-1.725+2}{11.5-1.725+2}=\frac{0.275}{11.775}\)≅0.023
Sanfoundry Global Education & Learning Series – Engineering Hydrology.
To practice all areas of Engineering Hydrology, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
