This set of Engineering Hydrology Multiple Choice Questions & Answers (MCQs) focuses on “Synthetic Unit Hydrograph – Set 3”.
1. The lag time for a watershed in mountainous region is given by,
t=1.715.\((\frac{LL_{ca}}{\sqrt{s}})^{0.38}\)
where, t is in hours, lengths are in km and S is the slope of the watershed. If the slope is increased by 33%, then what will be the ratio of the new lag time to the original lag time?
a) 0.95
b) 1.00
c) 1.06
d) 1.13
View Answer
Explanation: As per the given equation, the lag time varies with the slope as,
t∝\((\frac{1}{\sqrt{S}})^{0.38}\) ⇒ t∝S-0.19
Let the new lag time be ‘t1’ and the new slope be ‘S1’. So,
\(\frac{t_1}{t}=\frac{S_1^{-0.19}}{S^{-0.19}} = \frac{(1.33*S)^{-0.19}}{(S)^{-0.19}}\) =(1.33)-0.19=0.9473
→ \(\frac{t_1}{t}\)≅0.95
Therefore, the required ratio is 0.95.
2. What will be the time base for the synthetic unit hydrograph constructed by Snyder’s method for an effective storm of 2.6 hour standard duration occurring over the catchment?
a) 4 days
b) 98 hours
c) 115 hours
d) 6 days
View Answer
Explanation: Since the storm occurring over the catchment is of standard duration, the lag time is given by t=D*5.5=2.6*5.5=14.3 hours
Now the base time, tb=(3+\(\frac{t_{act}}{8}\))days = 3+\(\frac{14.3}{8}\) = 4.7875≅4.8 days
Or tb=(72+(3*tact)) hours = 72+(3*14.3)=114.9 hours≅115 hours.
3. The following synthetic unit hydrograph represents a rainfall of standard duration occurring over a catchment with regional constant 0.65. The area of the catchment is 580 km2. Find the value of Q (in cumecs).
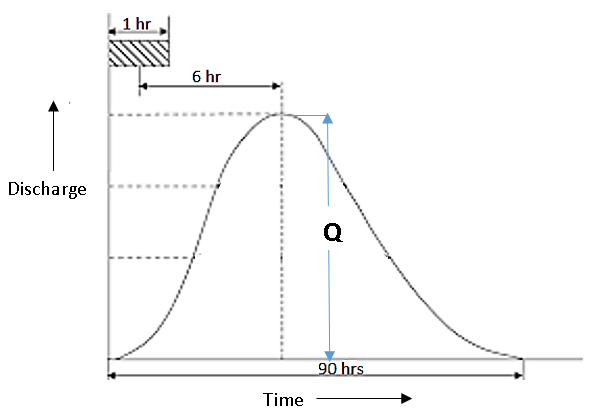
a) 12
b) 175
c) 385
d) 1065
View Answer
Explanation: It is given that the occurred rainfall is of standard duration, so the lag time need not be modified. The quantity Q standard peak discharge value and is given by,
Q=\(\frac{2.78*C_p*A}{t}=\frac{2.78*0.65*580}{6}\)=174.67 cumecs ≅175 cumecs
4. The following figure shows a rectangular basin of area 432 km2 with a main stream passing along its diagonal. Assume Snyder’s catchment constant as 1.40. Find the basin lag time (in hours, rounded off to the nearest integer) for the given catchment.
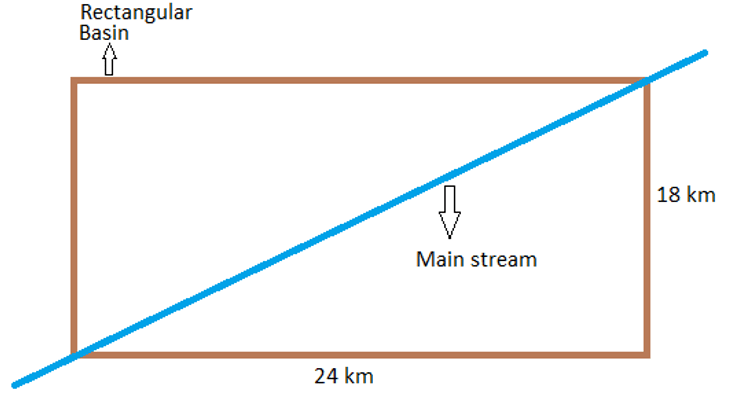
a) 7
b) 8
c) 9
d) 10
View Answer
Explanation: The lag time is given as,
t=Ct.(LLca)0.3
Since, stream passes along diagonal, L = length of diagonal = \(\)\sqrt{24^2+18^2}=\sqrt{900}=30 km
Also since the diagonal passes through the centroid, Lca = 30/2 = 15 km. So,
t=1.4*(30*15)0.3=8.75 hours ≈ 9 hours
5. The time base (in hours) for a synthetic UH is given as,
tb=5*(t+\(\frac{D}{2}\))
where, t and D represent the actual lag time and actual rainfall duration respectively, in hours. If the standard rainfall duration is 30 mins and actual rainfall is 60 mins, what will be the percentage error in time base if calculated as per standard results?
a) 11.11%
b) 12.50%
c) 15.00%
d) 16.87%
View Answer
Explanation: Let tb be the actual time base and tbs be the time base calculated using standard values.
Case 1: Using standard values.
Dstd=0.5 hour and tstd=5.5*Dstd=5.5*0.5=2.75 hours
→ tbs=5*(2.75+\(\frac{0.5}{2}\))=15 hours
Case 2: Using actual values.
D=1 hour and t=tstd+\((\frac{D-D_{std}}{4})\)=2.75+\((\frac{1-0.5}{4})\)=2.875 hours
→ tb=5*(2.875+\(\frac{1}{2}\))=16.875 hours
Therefore the percentage error is,
=\(\frac{(Actual \, value)-(Standard \, value)}{(Actual \, value)}\)*100
=\(\frac{16.875-15}{16.875}\)*100
=11.11%
6. The equation for calculating the width of UH (in hours) at 50% of peak discharge is given by the US Army Corps of Engineers as
W50=\(\frac{5.87}{q^{1.08}} \)
What is the dimensional representation of the quantity ‘q’ in the above equation?
a) LT-1
b) L3T-1
c) L2T-1
d) LT-2
View Answer
Explanation: The above equation relates the width of unit hydrograph to the peak discharge intensity. The term ‘q’ is the peak discharge per unit area of the catchment and has unit of m3/s/km2 which can be dimensionally represented as L3/T/L2 or L/T.
7. As per the equations given by the US Army Corps of Engineers, the width of unit hydrograph at 75% of peak discharge is less than 50% of that of the width of the unit hydrograph at 50% of peak discharge.
a) True
b) False
View Answer
Explanation: The width of the unit hydrograph corresponding to 75% of peak discharge is given as,
W75=\(\frac{W_{50}}{1.75}\)=0.5714*W50≅57% of W50
where, W50 is the width of unit hydrograph at 50% of peak discharge. From the above relation , it can be observed that W75 is more than 50% of W50.
8. The following figure shows a synthetic unit hydrograph for a storm over a catchment. Find the width (in hours) of the hydrograph corresponding to a discharge of 22 m3/s.
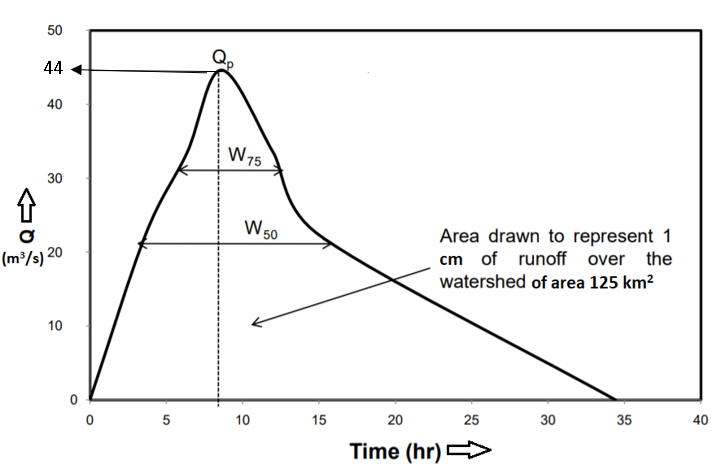
a) 12
b) 14
c) 16
d) 18
View Answer
Explanation: The peak discharge is given as 44 m3/s, which means that 22m3/s is the discharge value which is 50% of the peak. So,
W@22m3/s=\(\frac{5.87}{(\frac{Q_p}{A})^{1.08}} = \frac{5.87}{(\frac{44}{125})^{1.08}}\) = 18.13 hours≅18 hours
Sanfoundry Global Education & Learning Series – Engineering Hydrology.
To practice all areas of Engineering Hydrology, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
