This set of Engineering Hydrology Multiple Choice Questions & Answers (MCQs) focuses on “Groundwater – Equation of Motion – Set 2”.
1. What is the shape of the water table of an aquifer without recharge, located between two water bodies at different surface elevations?
a) Linear
b) Circular
c) Parabolic
d) Elliptical
View Answer
Explanation: The piezometric head for the above condition as per Dupit’s assumptions is given as,
h2=\(\frac{(h_1^2-h_0^2)}{L} x+h_0^2\)
Where K is the permeability, h0 and h1 the heads of the two water bodies respectively, L is the length of the aquifer and x is the distance from the upstream end. This equation represents a parabola, specifically known as Dupit’s parabola.
2. What is the shape of the water table of a constantly recharged unconfined aquifer present between two tile drains?
a) 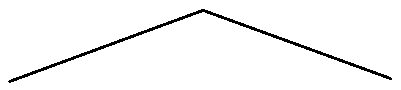
b) 
c) 
d) 
View Answer
Explanation: The head equation for the given condition can be derived by assuming the head of the water bodies, in this case tile drains, to be negligibly small (h0 =0, h1 = 0). So,
h2=\(\frac{R}{K} (L-x)x\)
Where R is the recharge rate, K is the permeability, L is the distance between tile drains and x is the distance from the one tile drain. This is equation represents a parabola.
3. Which of the following is true for an unconfined aquifer with top recharge present between two water bodies?
a) Water table is a parabola
b) Discharge per unit width of aquifer is constant
c) The flow is unidirectional
d) The water can lie anywhere in the aquifer between the two water bodies
View Answer
Explanation: The water table profile for the given aquifer is elliptical with a water divide at some location which splits the flow in two directions. The discharge per width varies throughout the width of the aquifer.
4. A confined aquifer of thickness 12 m is present between two parallel streams 2.5 km apart. The depths of the streams are 18 m and 14 m. If the permeability of the aquifer is 8 m/day, what is the flow per meter width of the aquifer?
a) 0.15 m3/day
b) 0.27 m3/day
c) 0.49 m3/day
d) 0.67 m3/day
View Answer
Explanation: Given h0 = 18 m, h1 = 14 m, B = 12 m, L = 2500m, K = 8 m/day
The flow per unit width is given as,
q=\(\frac{(h_0-h_1)}{L} KB=\frac{(18-14)}{2500}*8*12\)=1.6*10-3*96=0.1536 m3/day per m≅0.15 m3/day per m
5. The discharge per unit length of a tile drain in an unconfined aquifer is directly proportional to the distance between two consecutive drains for a given rate of recharge.
a) True
b) False
View Answer
Explanation: The discharge per unit length of a tile drain is q=RL, where R is the recharge rate and L is the distance between tile drains. It can be seen that for a given recharge, the discharge increases as the distance between tile drains increases.
6. The maximum height of the water table between two tile drains does not depend on which of the following?
a) Distance between the drains
b) Permeability of aquifer
c) Rate of recharge
d) Depth of aquifer
View Answer
Explanation: The maximum height of the water table between two tile drains occurs at the mid-point of the two drains. The height at that point is given as, hmax=\(\frac{L}{2}\sqrt{\frac{R}{K}}\).
7. Two rivers of depths 22 m and 17 m are connected by an unconfined aquifer of width 1370 m and permeability 7.5 m/day. The recharge rate per m2 of the aquifer area if the water divide lies on the upstream edge of the aquifer is k x 10-4 m3/day. What is the value of ‘k’?
a) 1.95
b) 3.87
c) 7.79
d) 15.58
View Answer
Explanation: Given h0 = 22 m, h1 = 17 m, L = 1370m, K = 7.5 m/day
If the water divide lies at the upstream end (x = 0), then a = 0.
a=\(\frac{L}{2}-\frac{K}{R} (\frac{h_0^2-h_1^2}{2L})\)=0
⇒\(\frac{L}{2}=\frac{K}{R}(\frac{h_0^2-h_1^2}{2L})\)
⇒R=\(\frac{K}{L^2} (h_0^2-h_1^2 )=\frac{7.5}{1370^2} (22^2-17^2 )=7.79*10^{-4} m^3/day/m^2\).
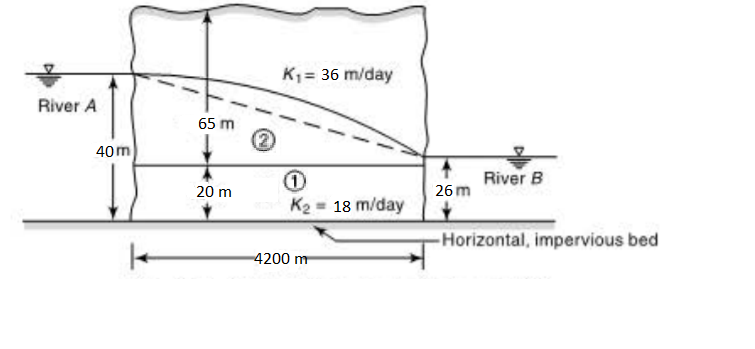
8. For the aquifer system shown (1 is confined aquifer and 2 is unconfined aquifer), find the total seepage discharge from river A to river B per meter width of the aquifer.
a) 2.64 m3/day
b) 3.04 m3/day
c) 6.02 m3/day
d) 9.12 m3/day
View Answer
Explanation: This is a composite aquifer system.
Firstly for confined aquifer (1), h0 = 40 m, h1 = 26 m, L = 4200m, K = 18 m/day, B =20 m.
q1=\(\frac{(h_0-h_1)}{L} KB=\frac{(40-26)}{4200}*18*20\)=1.2 m3/day/m
Secondly for unconfined aquifer (2), h0 = 40 – 20 = 20 m, h1 = 26 – 18 = 8 m, L = 4200m, K = 36 m/day.
q2=\(\frac{(h_0^2-h_1^2)}{2L} K=\frac{(20^2-8^2)}{2*4200}*36\)=1.44 m3/day/m
∴Total discharge=q1+q2=1.2+1.44=2.64 m3/day/m
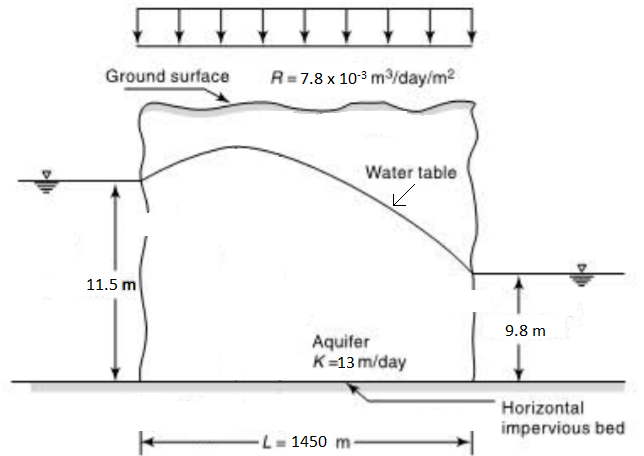
9. In the aquifer system shown, find the height of the water divide from the horizontal impervious bed.
a) 15 m
b) 17.5 m
c) 20 m
d) 22.5 m
View Answer
Explanation: Given h0 = 11.5 m, h1 = 19.8 m, L = 1450m, K = 13 m/day, R = 0.0078 m3/day/m2
For the given system, the water table profile is given as,
h2=-\(\frac{Rx^2}{K}-\frac{(h_0^2-h_1^2-\frac{RL^2}{K})}{L} x+h_0^2\)
=\(-(\frac{0.078}{13}) x^2-\frac{1}{1450} (11.5^2-9.8^2-\frac{0.0078*1450^2}{13})x+11.5^2\)
⇒h2=-0.0006x2+0.845x+132.25⋯⋯⋯(1)
Location of water table divide is given as,
a=\(\frac{L}{2}-\frac{K}{R} (\frac{h_0^2-h_1^2}{2L})=\frac{1450}{2}-\frac{13}{0.0078}(\frac{11.5^2-9.8^2}{2*1450})=704.19 m\) from upstream
Now substituting x = 7014.19 m in (1) we get,
\(h_{max}^2\)=-0.0006(704.19)2+0.845(704.19)+132.25=429.76
∴hmax=\(\sqrt{429.76}\)=20.73 m≅20 m
10. A tile drain system is installed in an unconfined aquifer of permeability 20 m/day and subjected to recharge of 0.005 m3/day/m2 of aquifer area. The drains are uniformly spaced at a distance of 500 m. Which of the following regarding the system is correct?
a) Water table profile is h2=0.00025x2-0.125x
b) Maximum height of water table is 4 m
c) Maximum water table height occurs at 125 m from a drain
d) Discharge entering a drain per m length is 1.25 m3/day
View Answer
Explanation: Given K = 20 m/day, R = 0.005 m3/day/m2, L = 500 m
The water table profile is,
h2=\(\frac{R}{K} (L-x)x=\frac{0.005}{20} (500-x)x\)=0.00025(500x-x2)
⇒h2=-0.00025x2+0.125x
Maximum height of water table is,
hmax=\(\frac{L}{2} \sqrt{\frac{R}{K}}=\frac{500}{2} \sqrt{\frac{0.005}{20}}=250\sqrt{0.00025}=3.95 m≅4 m\)
Discharge entering a drain is,
q=RL=0.005*500=2.5 m3/day per m length of drain
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
