This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “KD Tree”.
1. In what time can a 2-d tree be constructed?
a) O(N)
b) O(N log N)
c) O(N2)
d) O(M log N)
View Answer
Explanation: A perfectly balanced 2-d tree can be constructed in O(N log N) time. This value is computed mathematically.
2. Insertion into a 2-d tree is a trivial extension of insertion into a binary search tree.
a) true
b) false
View Answer
Explanation: Insertion of elements in a 2-d tree is similar to that of a binary search tree. Hence, it is a trivial extension of the binary search tree.
3. In a two-dimensional search tree, the root is arbitrarily chosen to be?
a) even
b) odd
c) depends on subtrees
d) 1
View Answer
Explanation: In a two- dimensional k-d tree (i.e.) 2-d tree, the root is arbitrarily chosen to be an odd level and it applies to all 2-d trees.
4. Which of the following is the simplest data structure that supports range searching?
a) Heaps
b) binary search trees
c) AA-trees
d) K-d trees
View Answer
Explanation: K-d trees are the simplest data structure that supports range searching and also it achieves the respectable running time.
5. In a k-d tree, k originally meant?
a) number of dimensions
b) size of tree
c) length of node
d) weight of node
View Answer
Explanation: Initially, 2-d trees were created. Then, 3-d trees, 4-trees etc., where k meant the number of dimensions.
6. What will be the correct sequence of insertion for the following k-d tree?
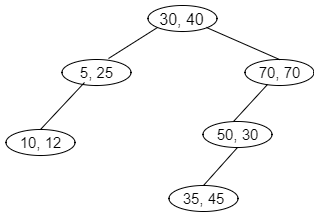
a) (30,40),(5,25),(70,70),(10,12),(50,30),(35,45)
b) (40,30),(5,25),(12,10),(70,70),(30,50),(45,35)
c) (30,40),(5,25),(10,12),(70,70),(50,30),(35,45)
d) (40,30),(25,5),(12,10),(70,70),(50,30),(45,35)
View Answer
Explanation: The correct sequence of insertion of the above given tree is (30,40),(5,25),(10,12),(70,70),(50,30),(35,45). The insertion is given by, first left, then right.
7. Each level in a k-d tree is made of?
a) dimension only
b) cutting and dimension
c) color code of node
d) size of the level
View Answer
Explanation: Each level in a k-d tree is made of dimensions and cutting. Cutting and dimensions are used for insertion, deletion and searching purposes.
8. What is the worst case of finding the nearest neighbour?
a) O(N)
b) O(N log N)
c) O( log N)
d) O(N3)
View Answer
Explanation: The worst case analysis of finding the nearest neighbour in a k-d tree is mathematically found to be O(N).
9. What is the run time of finding the nearest neighbour in a k-d tree?
a) O(2+ log N)
b) O( log N)
c) O(2d log N)
d) O( N log N)
View Answer
Explanation: The run time of finding the nearest neighbour in a kd tree is given as O(2d log N) where 2d is the time taken to search the neighbourhood.
10. How many prime concepts are available in nearest neighbour search in a kd tree?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: Three important concepts are available in finding the nearest neighbour. They are partial results, pruning, traversal order.
11. Reducing search space by eliminating irrelevant trees is known as?
a) pruning
b) partial results
c) freeing space
d) traversing
View Answer
Explanation: Pruning is eliminating irrelevant trees. Partial results are keeping best results and updating. Traversal is visiting all the nodes of a tree.
12. Several kinds of queries are possible on a k-d called as?
a) partial queries
b) range queries
c) neighbour queries
d) search queries
View Answer
Explanation: Several range queries are possible on a k-d tree. One of the range queries is known as a partial match query.
13. What is the time taken for a range query for a perfectly balanced tree?
a) O(N)
b) O(log N)
c) O(√N+M)
d) O(√N)
View Answer
Explanation: For a perfectly balanced k-d tree, the range query could take O(√N+M) in the worst case to report M matches.
14. The 2d search tree has the simple property that branching on odd levels is done with respect to the first key.
a) True
b) False
View Answer
Explanation: Branching on odd levels is done with respect to the first key and branching on even levels is done with respect to the second key in a 2-d tree.
15. Who invented k-d trees?
a) Arne Andersson
b) Jon Bentley
c) Jon Von Newmann
d) Rudolf Bayer
View Answer
Explanation: Jon Bentley found k-d trees. Rudolf Bayer found red black trees. Arne Andersson found AA- trees.
Sanfoundry Global Education & Learning Series – Data Structure.
To practice all areas of Data Structure, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Programming Books
- Apply for Computer Science Internship
- Practice Design & Analysis of Algorithms MCQ
- Check Data Structure Books
- Check Computer Science Books
