This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Min/Max Heap”.
1. Descending priority queue can be implemented using ______
a) max heap
b) min heap
c) min-max heap
d) trie
View Answer
Explanation: Descending priority queue arranges the elements based on their priority or value and allows removing the elements in descending order. So, it can be efficiently implemented using max heap.
2. Min heap can be used to implement selection sort.
a) True
b) False
View Answer
Explanation: In min heap, the insertion and deletion operation takes O(logn) time. Therefore, a selection sort with n insertions and n deletions can be implemented using a min heap in O(nlogn) operations.
3. Which of the following is the valid min heap?
a)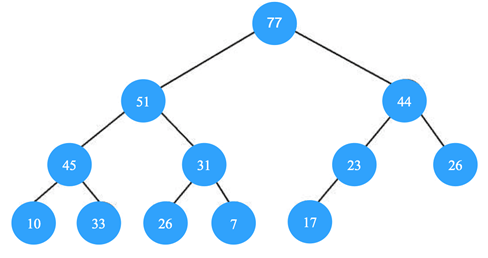
b)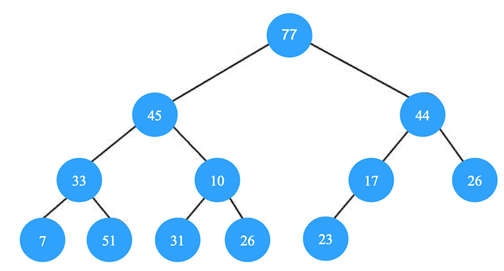
c)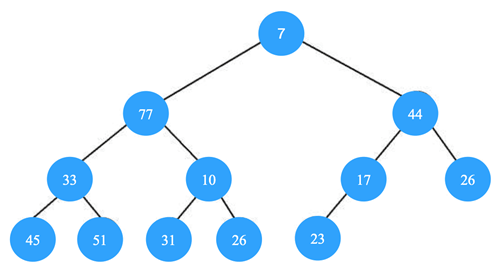
d)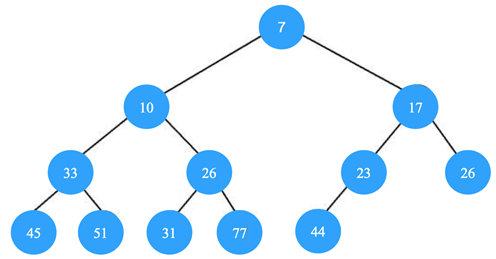
View Answer
Explanation: In min heap the smallest is located at the root and the largest elements are located at the leaf nodes. So, all leaf nodes need to be checked to find the largest element.
4. The procedure given below is used to maintain min-order in the min heap. Find out the missing statements, represented as X.
procedure TrickleDownMin(i) if A[i] has children then m := index of smallest of the children or grandchildren (if any) of A[i] if A[m] is a grandchild of A[i] then if A[m] < A[i] then swap A[i] and A[m] X: _______________________ ____________________ endif TrickleDownMin(m) endif else //{A[m] is a child of A[i]} if A[m] < A[i] then swap A[i] and A[m] endif endif
a) if A[m] > A[parent(m)] then
swap A[m] and A[parent(m)]
b) if A[m] > A[parent(m)] then
swap A[i] and A[parent(m)]
c) if A[m] < A[parent(m)] then
swap A[m] and A[parent(m)]
d) if A[m] > A[parent(m)] then
swap A[i] and A[parent(m)]
View Answer
Explanation: In TrickleDownMin() procedure, we maintain the min-ordering of the min heap. In this procedure, we locate the lowest child or grandchild of the element at positions i. If the lowest element is grandchild then we check that it is smaller than both, its parent and A[i].
5. The ascending heap property is ___________
a) A[Parent(i)] =A[i]
b) A[Parent(i)] <= A[i]
c) A[Parent(i)] >= A[i]
d) A[Parent(i)] > 2 * A[i]
View Answer
Explanation: The min heap is also known as ascending heap. Min heap of size n is an almost complete binary tree of n nodes such that the element at each node is greater than or equal to the element at its parent node.
6. The procedure FindMin() to find the minimum element and the procedure DeleteMin() to delete the minimum element in min heap take _________
a) logarithmic and linear time constant respectively
b) constant and linear time respectively
c) constant and quadratic time respectively
d) constant and logarithmic time respectively
View Answer
Explanation: In the min heap, the root is the maximum element in the tree. So, locating it takes constant time, but deleting it takes logarithmic time. Because after deleting it, the root is replaced with last element and then the procedure to maintain the min ordering is invoked.
7. Which one of the following array elements represents a binary min heap?
a) 12 10 8 25 14 17
b) 8 10 12 25 14 17
c) 25 17 14 12 10 8
d) 14 17 25 10 12 8
View Answer
Explanation: A tree is min heap when data at every node in the tree is smaller than or equal to it’s children’ s data. So, only 8 10 12 25 14 17 generates required tree.
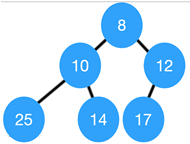
8. In a binary min heap containing n elements, the largest element can be found in __________ time.
a) O(n)
b) O(nlogn)
c) O(logn)
d) O(1)
View Answer
Explanation: In min heap the smallest is located at the root and the largest elements are located at the leaf nodes. So, all leaf nodes need to be checked to find the largest element. Thus, worst case time will be O (n).
9. Min heap is a complete binary tree.
a) True
b) False
View Answer
Explanation: A tree, in which all levels are fully filled, except possibly the last level, is called as the complete binary tree. And min heap maintains shape property, so it is a complete binary tree. The shape property ensures that all levels in the min heap are fully filled, except the last one, and, if the last level is not filled completely, then fill the elements from left to right.
10. What will be the position of 5, when a max heap is constructed on the input elements 5, 70, 45, 7, 12, 15, 13, 65, 30, 25?
a) 5 will be at root
b) 5 will be at last level
c) 5 will be at second level
d) 5 can be anywhere in heap
View Answer
Explanation: In max heap the greatest element is at the root and the smallest elements are at the last level. As 5 is the smallest input element, it will be at the last level.
Sanfoundry Global Education & Learning Series – Data Structure.
To practice all areas of Data Structure, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Check Computer Science Books
- Check Data Structure Books
- Check Programming Books
- Practice Design & Analysis of Algorithms MCQ
- Practice Programming MCQs
