This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Cartesian Tree”.
1. What is a Cartesian tree?
a) a skip list in the form of tree
b) a tree which obeys cartesian product
c) a tree which obeys heap property and whose inorder traversal yields the given sequence
d) a tree which obeys heap property only
View Answer
Explanation: A tree with heap property (parent is either small or big than children) and when traversed in inorder yields the given input sequence. refer below diagram question for clarity.
2. Is the below tree representation of 50,100,400,300,280 correct way to represent cartesian tree?
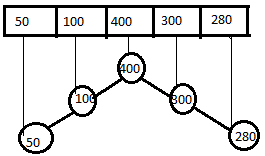
a) true
b) false
View Answer
Explanation: A tree with heap property (parent is either small or big than children) and when traversed in inorder yields the given input sequence is called as a cartesian tree. as the above figure satisies both the properties. note that even min heap tree can be generated. the above is a max heap tree.
3. Which of the below statements are true?
i. Cartesian tree is not a height balanced tree
ii. Cartesian tree of a sequence of unique numbers can be unique generated
a) both statements are true
b) only i. is true
c) only ii. is true
d) both are false
View Answer
Explanation: A height balanced cartesian tree is not possible as seen in above question. also any time a unique sequnce possess a unique cartesian tree, this can be proven through induction.
4. What is the speciality of cartesian sorting?
a) it sorts partially sorted set of data quickly
b) it considers cartesian product of elements
c) it sorts elements in less than O(logn)
d) it is a self balancing tree
View Answer
Explanation: It can sort a set which requires only some sorting or displacements. for example consider 78, 79, 80, 82, 81, 83, In this only 81 and 82 must be swaped to make it a complete sorted set, in this case cartesian sort comes to the rescue.
5. Consider a sequence of numbers to have repetitions, how a cartesian tree can be constructed in such situations without violating any rules?
a) use any tie-breaking rule between repeated elements
b) cartesian tree is impossible when repetitions are present
c) construct a max heap in such cases
d) construct a min heap in such cases
View Answer
Explanation: Consider any of the tie breaking rules, for example the element which appears first can be taken as small among the same elements and then apply cartesian tree rules.
6. What happens if we apply the below operations on an input sequence?
i. construct a cartesian tree for input sequence
ii. put the root element of above tree in a priority queue
iii. if( priority queue is not empty) then
iv. search and delete minimum value in priority queue
v. add that to output
vi. add cartesian tree children of above node to priority queue
a) constructs a cartesian tree
b) sorts the input sequence
c) does nothing
d) produces some random output
View Answer
Explanation: The above given steps are for sorting a cartesian tree. cartesian sort is benificial in case of partially sorted set of elements. a cartesian sort can be considered as a selection or heap sort maintaing a priority queue.
7. Cartesian trees are most suitable for?
a) searching
b) finding nth element
c) minimum range query and lowest common ancestors
d) self balancing a tree
View Answer
Explanation: In a cartesian tree minimum value can be found by finding lowest common ancestor for the extreme elements. consider 11,9,19,16 the lowest element is 9 and is a lowest common ancestor for 11 and 16. and by applying few techniques cartesian tree can be used to even find lowest common ancestors efficiently.
these can be done in constant time. tree can be constructed in linear time (this is the most efficient time for any tree construction) and takes space as many elements are there.
8. A treap is a cartesian tree with ___________
a) additional value, which is a priority value to the key generated randomly
b) additional value, which is a priority value to the key generated sequentially
c) additional heap rule
d) additional operations like remove a range of elements
View Answer
Explanation: A cartesian tree, if feeded with a sorted sequence will generate a straight path (or in tree terminology a skew tree). moreover a cartesian tree basing on same values from the search keys doesnot work well. so a cartesian tree with priority value in addition to search key is called treap.
9. Cartesian trees solve range minimum query problem in constant time.
a) true
b) false
View Answer
Explanation: Range minmum query is finding the minimum element in a given subarray of an array. Constant time is achieved by storing the Cartesian trees for all the blocks in the array. Rmq’s are used in string matchings, computing lowest common ancestor and longest common prefix of a sring.
10. Consider below sequences.
array=60 90 10 100 40 150 90 reverse 2 to 3 array=60 10 90 100 40 150 90 reverse 3 to 6 array= 60 100 150 40 100 90 90 now printout from 1 to 6 :-- 60 100 150 40 100 90
How to achieve the above operation efficiently?
a) use linked lists
b) use avl trees
c) use red-black trees
d) use treaps (cartesian trees)
View Answer
Explanation: This can be solved efficiently using treap which is a modification of cartesian tree. an attribute like “boolean reverse” can be maintained with every node representing whether to reverse or not.
Sanfoundry Global Education & Learning Series – Data Structure.
To practice all areas of Data Structure, here is complete set of 1000+ Multiple Choice Questions and Answers.
- Practice Computer Science MCQs
- Practice Programming MCQs
- Practice Design & Analysis of Algorithms MCQ
- Check Data Structure Books
- Check Computer Science Books
