This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “AVL Tree”.
1. What is an AVL tree?
a) a tree which is balanced and is a height balanced tree
b) a tree which is unbalanced and is a height balanced tree
c) a tree with three children
d) a tree with atmost 3 children
View Answer
Explanation: It is a self balancing tree with height difference atmost 1.
2. Why we need to a binary tree which is height balanced?
a) to avoid formation of skew trees
b) to save memory
c) to attain faster memory access
d) to simplify storing
View Answer
Explanation: In real world dealing with random values is often not possible, the probability that u are dealing with non random values(like sequential) leads to mostly skew trees, which leads to worst case. hence we make height balance by rotations.
3. Which of the below diagram is following AVL tree property?
i.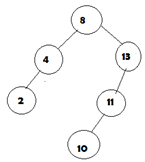
ii.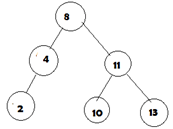
a) only i
b) only i and ii
c) only ii
d) i is not a binary search tree
View Answer
Explanation: The property of AVL tree is it is height balanced tree with difference of atmost 1 between left and right subtrees. All AVL trees are binary search tree.
4. What is the maximum height of an AVL tree with p nodes?
a) p
b) log(p)
c) log(p)/2
d) p⁄2
View Answer
Explanation: Consider height of tree to be ‘he’, then number of nodes which totals to p can be written in terms of height as N(he)=N(he-1)+1+N(he-2). since N(he) which is p can be written in terms of height as the beside recurrence relation which on solving gives N(he)= O(logp) as worst case height.
5. To restore the AVL property after inserting a element, we start at the insertion point and move towards root of that tree. is this statement true?
a) true
b) false
View Answer
Explanation: It is interesting to note that after insertion, only the path from that point to node or only that subtrees are imbalanced interms of height.
6. Given an empty AVL tree, how would you construct AVL tree when a set of numbers are given without performing any rotations?
a) just build the tree with the given input
b) find the median of the set of elements given, make it as root and construct the tree
c) use trial and error
d) use dynamic programming to build the tree
View Answer
Explanation: Sort the given input, find the median element among them, make it as root and construct left and right subtrees with elements lesser and greater than the median element recursively. this ensures the subtrees differ only by height 1.
7. What maximum difference in heights between the leafs of a AVL tree is possible?
a) log(n) where n is the number of nodes
b) n where n is the number of nodes
c) 0 or 1
d) atmost 1
View Answer
Explanation: At every level we can form a tree with difference in height between subtrees to be atmost 1 and so there can be log(n) such levels since height of AVL tree is log(n).
8. Consider the pseudo code:
int avl(binarysearchtree root): if(not root) return 0 left_tree_height = avl(left_of_root) if(left_tree_height== -1) return left_tree_height right_tree_height= avl(right_of_root) if(right_tree_height==-1) return right_tree_height
Does the above code can check if a binary search tree is an AVL tree?
a) yes
b) no
View Answer
Explanation: The condition to check the height difference between left and right subtrees is missing. if (absolute(left_tree_height – right_tree_height)>1) must be added.
9. Consider the below left-left rotation pseudo code where the node contains value pointers to left, right child nodes and a height value and Height() function returns height value stored at a particular node.
avltree leftrotation(avltreenode z): avltreenode w =x-left x-left=w-right w-right=x x-height=max(Height(x-left),Height(x-right))+1 w-height=max(missing)+1 return w
What is missing?
a) Height(w-left), x-height
b) Height(w-right), x-height
c) Height(w-left), x
d) Height(w-left)
View Answer
Explanation: In the code we are trying to make the left rotation and so we need to find maximum of those two values.
10. Why to prefer red-black trees over AVL trees?
a) Because red-black is more rigidly balanced
b) AVL tree store balance factor in every node which costs space
c) AVL tree fails at scale
d) Red black is more efficient
View Answer
Explanation: Every node in an AVL tree need to store the balance factor (-1, 0, 1) hence space costs to O(n), n being number of nodes. but in red-black we can use the sign of number (if numbers being stored are only positive) and hence save space for storing balancing information. there are even other reasons where redblack is mostly prefered.
Sanfoundry Global Education & Learning Series – Data Structure.
To practice all areas of Data Structure, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Computer Science Books
- Practice Programming MCQs
- Practice Design & Analysis of Algorithms MCQ
- Apply for Computer Science Internship
- Check Programming Books
