Data Structure Questions and Answers – Adjacency Matrix

This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Adjacency Matrix”.

1. The number of elements in the adjacency matrix of a graph having 7 vertices is __________
a) 7
b) 14
c) 36
d) 49
View Answer

2. What would be the number of zeros in the adjacency matrix of the given graph?

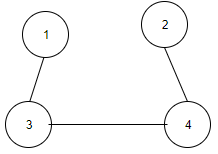
a) 10
b) 6
c) 16
d) 0
View Answer

   1  2  3  4
1  0  0  1  0
2  0  0  0  1
3  1  0  0  1
4  0  1  1  0

3. Adjacency matrix of all graphs are symmetric.
a) False
b) True
View Answer

4. The time complexity to calculate the number of edges in a graph whose information in stored in form of an adjacency matrix is ____________
a) O(V)
b) O(E²)
c) O(E)
d) O(V²)
View Answer

5. For the adjacency matrix of a directed graph the row sum is the _________ degree and the column sum is the ________ degree.
a) in, out
b) out, in
c) in, total
d) total, out
View Answer

6. What is the maximum number of possible non zero values in an adjacency matrix of a simple graph with n vertices?
a) (n*(n-1))/2
b) (n*(n+1))/2
c) n*(n-1)
d) n*(n+1)
View Answer

7. On which of the following statements does the time complexity of checking if an edge exists between two particular vertices is not, depends?
a) Depends on the number of edges
b) Depends on the number of vertices
c) Is independent of both the number of edges and vertices
d) It depends on both the number of edges and vertices
View Answer

8. In the given connected graph G, what is the value of rad(G) and diam(G)?
a) 2, 3
b) 3, 2
c) 2, 2
d) 3, 3
View Answer

9. Which of these adjacency matrices represents a simple graph?
a) [ [1, 0, 0], [0, 1, 0], [0, 1, 1] ]
b) [ [1, 1, 1], [1, 1, 1], [1, 1, 1] ]
c) [ [0, 0, 1], [0, 0, 0], [0, 0, 1] ]
d) [ [0, 0, 1], [1, 0, 1], [1, 0, 0] ]
View Answer

10. Given an adjacency matrix A = [ [0, 1, 1], [1, 0, 1], [1, 1, 0] ], The total no. of ways in which every vertex can walk to itself using 2 edges is ________
a) 2
b) 4
c) 6
d) 8
View Answer

11. If A[x+3][y+5] represents an adjacency matrix, which of these could be the value of x and y.
a) x=5, y=3
b) x=3, y=5
c) x=3, y=3
d) x=5, y=5
View Answer

12. Two directed graphs(G and H) are isomorphic if and only if A=PBP-1, where P and A are adjacency matrices of G and H respectively.
a) True
b) False
View Answer

13. Given the following program, what will be the 3rd number that’d get printed in the output sequence for the given input?

#include <bits/stdc++.h> 
using namespace std; 
int cur=0; 
int G[10][10]; 
bool visited[10]; 
deque <int> q; 
 
void fun(int n); 
 
int main()
{   
	int num=0; 
	int n; 
	cin>>n; 
 
	for(int i=0;i<n;i++) 
      	for(int j=0;j<n;j++) 
        	cin>>G[i][j]; 
 
	for(int i=0;i<n;i++) 
        visited[i]=false; 
 
        fun(n); 
	return 0; 
} 
 
void fun(int n)
{ 
	cout<<cur<<" "; 
	visited[cur]=true; 
	q.push_back(cur); 
 
	do
        { 
		for(int j=0;j<n;j++)
                { 
		    if(G[cur][j]==1 && !visited[j])
                    { 
		        q.push_back(j); 
		        cout<<j<<" "; 
		        visited[j]=true; 
	            } 
 
                 } 
 
		q.pop_front(); 
		if(!q.empty()) 
		cur=q.front(); 
	 }while(!q.empty()); 
}

Input Sequence:-

9 
0 1 0 0 0 0 0 0 1    
1 0 0 0 0 0 0 0 0 
0 0 0 1 1 1 0 0 1 
0 0 1 0 0 0 0 0 0 
0 0 1 0 0 0 0 1 0 
0 0 1 0 0 0 1 0 0 
0 0 0 0 0 1 0 1 1 
0 0 0 0 1 0 1 0 0 
1 0 1 0 0 0 1 0 0

a) 2
b) 6
c) 8
d) 4
View Answer

14. For which type of graph, the given program won’t run infinitely? The Input would be in the form of an adjacency Matrix and n is its dimension (1<n<10).

#include <bits/stdc++.h> 
using namespace std; 
int G[10][10]; 
void fun(int n); 
 
int main()
{
	int num=0; 
	int n; 
	cin>>n; 
	for(int i=0;i<n;i++) 
 		for(int j=0;j<n;j++) 
        		cin>>G[i][j]; 
    	fun(n); 
	return 0; 
}	 
 
void fun(int n)
{ 
	for(int i=0;i<n;i++) 
	for(int j=0;j<n;j++) 
	if(G[i][j]==1) 
	j--; 
}

a) All Fully Connected Graphs
b) All Empty Graphs
c) All Bipartite Graphs
d) All simple graphs
View Answer

15. Given the following adjacency matrix of a graph(G) determine the number of components in the G.

[0 1 1 0 0 0], 
[1 0 1 0 0 0],
[1 1 0 0 0 0],
[0 0 0 0 1 0],
[0 0 0 1 0 0],
[0 0 0 0 0 0].

a) 1
b) 2
c) 3
d) 4
View Answer

Sanfoundry Global Education & Learning Series – Data Structure.

To practice all areas of Data Structure, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]