This set of Data Structure Multiple Choice Questions & Answers (MCQs) focuses on “Binary Search Tree”.
1. Which of the following is false about a binary search tree?
a) The left child is always lesser than its parent
b) The right child is always greater than its parent
c) The left and right sub-trees should also be binary search trees
d) In order sequence gives decreasing order of elements
View Answer
Explanation: In order sequence of binary search trees will always give ascending order of elements. Remaining all are true regarding binary search trees.
2. How to search for a key in a binary search tree?
a)
public Tree search(Tree root, int key) { if( root == null || root.key == key ) { return root; } if( root.key < key ) { return search(root.right,key); } else return search(root.left,key); }
b)
public Tree search(Tree root, int key) { if( root == null || root.key == key ) { return root; } if( root.key < key ) { return search(root.left,key); } else return search(root.right,key); }
c)
public Tree search(Tree root, int key) { if( root == null) { return root; } if( root.key < key ) { return search(root.right,key); } else return search(root.left,key); }
d)
public Tree search(Tree root, int key) { if( root == null) { return root; } if( root.key < key ) { return search(root.right.right,key); } else return search(root.left.left,key); }
Explanation: As we know that the left child is lesser than the parent, if the root’s key is greater than the given key, we look only into the left sub-tree, similarly for right sub-tree.
3. What is the speciality about the inorder traversal of a binary search tree?
a) It traverses in a non increasing order
b) It traverses in an increasing order
c) It traverses in a random fashion
d) It traverses based on priority of the node
View Answer
Explanation: As a binary search tree consists of elements lesser than the node to the left and the ones greater than the node to the right, an inorder traversal will give the elements in an increasing order.
4. What does the following piece of code do?
public void func(Tree root) { func(root.left()); func(root.right()); System.out.println(root.data()); }
a) Preorder traversal
b) Inorder traversal
c) Postorder traversal
d) Level order traversal
View Answer
Explanation: In a postorder traversal, first the left child is visited, then the right child and finally the parent.
5. What does the following piece of code do?
public void func(Tree root) { System.out.println(root.data()); func(root.left()); func(root.right()); }
a) Preorder traversal
b) Inorder traversal
c) Postorder traversal
d) Level order traversal
View Answer
Explanation: In a preorder traversal, first the parent is visited, then the left child and finally the right child.
6. How will you find the minimum element in a binary search tree?
a)
public void min(Tree root) { while(root.left() != null) { root = root.left(); } System.out.println(root.data()); }
b)
public void min(Tree root) { while(root != null) { root = root.left(); } System.out.println(root.data()); }
c)
public void min(Tree root) { while(root.right() != null) { root = root.right(); } System.out.println(root.data()); }
d)
public void min(Tree root) { while(root != null) { root = root.right(); } System.out.println(root.data()); }
Explanation: Since all the elements lesser than a given node will be towards the left, iterating to the leftmost leaf of the root will give the minimum element in a binary search tree.
7. How will you find the maximum element in a binary search tree?
a)
public void max(Tree root) { while(root.left() != null) { root = root.left(); } System.out.println(root.data()); }
b)
public void max(Tree root) { while(root != null) { root = root.left(); } System.out.println(root.data()); }
c)
public void max(Tree root) { while(root.right() != null) { root = root.right(); } System.out.println(root.data()); }
d)
public void max(Tree root) { while(root != null) { root = root.right(); } System.out.println(root.data()); }
Explanation: Since all the elements greater than a given node are towards the right, iterating through the tree to the rightmost leaf of the root will give the maximum element in a binary search tree.
8. What are the worst case and average case complexities of a binary search tree?
a) O(n), O(n)
b) O(logn), O(logn)
c) O(logn), O(n)
d) O(n), O(logn)
View Answer
Explanation: Worst case arises when the tree is skewed(either to the left or right) in which case you have to process all the nodes of the tree giving O(n) complexity, otherwise O(logn) as you process only the left half or the right half of the tree.
9. Given that 2 elements are present in the tree, write a function to find the LCA(Least Common Ancestor) of the 2 elements.
a)
public void lca(Tree root,int n1, int n2) { while (root != NULL) { if (root.data() > n1 && root.data() > n2) root = root.right(); else if (root.data() < n1 && root.data() < n2) root = root.left(); else break; } System.out.println(root.data()); }
b)
public void lca(Tree root,int n1, int n2) { while (root != NULL) { if (root.data() > n1 && root.data() < n2) root = root.left(); else if (root.data() < n1 && root.data() > n2) root = root.right(); else break; } System.out.println(root.data()); }
c)
public void lca(Tree root,int n1, int n2) { while (root != NULL) { if (root.data() > n1 && root.data() > n2) root = root.left(); else if (root.data() < n1 && root.data() < n2) root = root.right(); else break; } System.out.println(root.data()); }
d)
public void lca(Tree root,int n1, int n2) { while (root != NULL) { if (root.data() > n1 && root.data() > n2) root = root.left.left(); else if (root.data() < n1 && root.data() < n2) root = root.right.right(); else break; } System.out.println(root.data()); }
Explanation: The property of a binary search tree is that the lesser elements are to the left and greater elements are to the right, we use this property here and iterate through the tree such that we reach a point where the 2 elements are on 2 different sides of the node, this becomes the least common ancestor of the 2 given elements.
10. What are the conditions for an optimal binary search tree and what is its advantage?
a) The tree should not be modified and you should know how often the keys are accessed, it improves the lookup cost
b) You should know the frequency of access of the keys, improves the lookup time
c) The tree can be modified and you should know the number of elements in the tree before hand, it improves the deletion time
d) The tree should be just modified and improves the lookup time
View Answer
Explanation: For an optimal binary search The tree should not be modified and we need to find how often keys are accessed. Optimal binary search improves the lookup cost.
11. Construct a binary search tree with the below information.
The preorder traversal of a binary search tree 10, 4, 3, 5, 11, 12.
a) 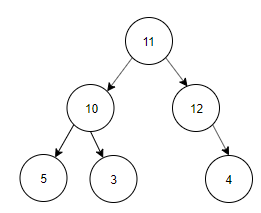
b) 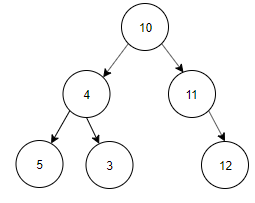
c) 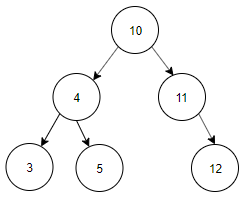
d) 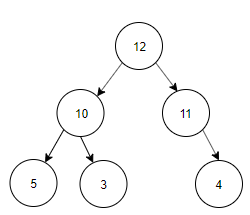
View Answer
Explanation: Preorder Traversal is 10, 4, 3, 5, 11, 12. Inorder Traversal of Binary search tree is equal to ascending order of the nodes of the Tree. Inorder Traversal is 3, 4, 5, 10, 11, 12. The tree constructed using Preorder and Inorder traversal is

Sanfoundry Global Education & Learning Series – Data Structure.
To practice all areas of Data Structure, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Computer Science Internship
- Practice Programming MCQs
- Check Data Structure Books
- Practice Computer Science MCQs
- Check Programming Books
