This set of Data Structures & Algorithms Multiple Choice Questions & Answers (MCQs) focuses on “Evaluation of a Postfix Expression”.
1. What is the other name for a postfix expression?
a) Normal polish Notation
b) Reverse polish Notation
c) Warsaw notation
d) Infix notation
View Answer
Explanation: Reverse polish Notation is the other name for a postfix expression whereas Polish Notation, Warsaw notation are the other names for a prefix expression.
2. Which of the following is an example for a postfix expression?
a) a*b(c+d)
b) abc*+de-+
c) +ab
d) a+b-c
View Answer
Explanation: abc*+de-+ is a postfix expression. +ab is a prefix expression and others are infix expressions.
3. Reverse Polish Notation is the reverse of a Polish Notation.
a) True
b) False
View Answer
Explanation: Reverse Polish Notation is not the reverse of a polish notation. Though both NPN and RPN read the expression from left to right, they follow different strategies.
4. What is the time complexity of evaluation of postfix expression algorithm?
a) O (N)
b) O (N log N)
c) O (N2)
d) O (M log N)
View Answer
Explanation: The time complexity of evaluation of infix, prefix and postfix expressions is O (N).
5. In Postfix expressions, the operators come after the operands.
a) True
b) False
View Answer
Explanation: In postfix expressions, the operators follow operands. In prefix expressions, the operands follow operators.
6. Which of these operators have the highest order of precedence?
a) ‘(‘ and ‘)’
b) ‘*’ and ‘/’
c) ‘~’ and ‘^’
d) ‘+’ and ‘-‘
View Answer
Explanation: The highest order of precedence is ~ and ^ followed by ‘*’ ,’ /’, ‘+’ ,’-‘ and then braces ‘(‘ ‘)’.
7. Which of the following is not an application of stack?
a) evaluation of postfix expression
b) conversion of infix to postfix expression
c) balancing symbols
d) line at ticket counter
View Answer
Explanation: Line at ticket counter is an application of queue whereas conversion of infix to postfix expression, balancing symbols, line at ticket counter are stack applications.
8. While evaluating a postfix expression, when an operator is encountered, what is the correct operation to be performed?
a) push it directly on to the stack
b) pop 2 operands, evaluate them and push the result on to the stack
c) pop the entire stack
d) ignore the operator
View Answer
Explanation: When an operator is encountered, the first two operands are popped from the stack, they are evaluated and the result is pushed into the stack.
9. Which of the following statement is incorrect?
a) Postfix operators use value to their right
b) Postfix operators use value to their left
c) Prefix operators use value to their right
d) In postfix expression, operands are followed by operators
View Answer
Explanation: All prefix operators use values to their right and all postfix operators use values to their left.
10. What is the result of the given postfix expression? abc*+ where a=1, b=2, c=3.
a) 4
b) 5
c) 6
d) 7
View Answer
Explanation: The infix expression is a+b*c. Evaluating it, we get 1+2*3=7.
11. What is the result of the following postfix expression?
ab*cd*+ where a=2,b=2,c=3,d=4.
a) 16
b) 12
c) 14
d) 10
View Answer
Explanation: The infix expression is a*b+c*d. Evaluating it, we get, 2*2+3*4=16.
12. Consider the stack
| 5 |
| 4 |
| 3 |
| 2 |.
At this point, ‘*’ is encountered. What has to be done?
a) 5*4=20 is pushed into the stack
b) * is pushed into the stack
c) 2*3=6 is pushed into the stack
d) * is ignored
View Answer
Explanation: When an operator is encountered, the first two operands of the stack are popped, evaluated and the result is pushed into the stack.
13. Evaluate the postfix expression ab + cd/- where a=5, b=4, c=9, d=3.
a) 23
b) 15
c) 6
d) 10
View Answer
Explanation: The infix expression is (a+b)-c/d. Evaluating it, (5+4)-9/3 gives 6.
14. Evaluate and write the result for the following postfix expression
abc*+de*f+g*+ where a=1, b=2, c=3, d=4, e=5, f=6, g=2.
a) 61
b) 59
c) 60
d) 55
View Answer
Explanation: The infix expression is a+b*c+(d*e+f)*g. Evaluating it, 1+2*3+(4*5+6)*2 gives 59.
15. For the given expression tree, write the correct postfix expression.
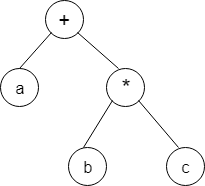
a) abc*+
b) abc+*
c) ab+c*
d) a+bc*
View Answer
Explanation: Evaluating the given expression tree gives the infix expression a+b*c. Converting it to postfix, we get, abc*+.
Sanfoundry Global Education & Learning Series – Data Structure.
To practice all areas of Data Structure, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Data Structure Books
- Practice Computer Science MCQs
- Check Computer Science Books
- Practice Design & Analysis of Algorithms MCQ
- Practice Programming MCQs
