This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “The Basic Normal Shock Equations – 1”.
1. A shock wave that is normal to the upstream flow is a rare case.
a) False
b) True
View Answer
Explanation: The normal shock wave, i.e. the one normal to the upstream flow, seems rare. But actually, it is a very frequent case of shock waves and occurs at many times in different cases.
2. The supersonic flow over a blunt body is given. Mark the area where the normal shock wave exists.
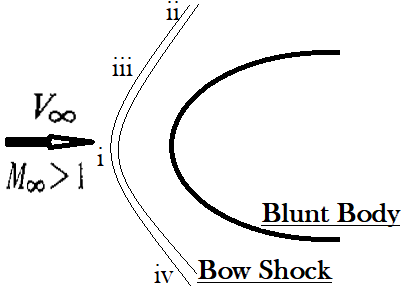
a) i
b) ii
c) iii
d) iv
View Answer
Explanation: In the figure, a strong bow shock exists in front of the flow. The shock wave is curved around the blunt body, but the region of the shock closest to the nose is essentially perpendicular to the flow, i.e. region i is a normal shock.
3. Which of these is incorrect for the normal shock wave analysis?
a) No viscous effects or body forces
b) Adiabatic flow
c) Differential form of conservation equations used
d) Steady flow
View Answer
Explanation: The normal shock wave analysis uses the control volume approach. The integral form of conservation equations are applied to the control volume. The flow is steady, adiabatic, without viscous effects and zero body forces.
4. Which is not true for continuity equation of normal shock?
a) ρ1u1A1=ρ2u2A2
b) ρ1u1=ρ2u2
c) Steady flow
d) No viscosity
View Answer
Explanation: The continuity equation of the normal shock equation is derived from the continuity equation of mass and is given as ρ1u1A1=ρ2u2A2. If the area of the control volume is same on both sides, it becomes ρ1u1=ρ2u2. The flow is steady and without viscosity.
5. The incorrect equation for the normal shock equation is_______
a) ρ1u1=ρ2u2
b) p1+ρ1u\(_1^2\)=p2+ρ2u\(_2^2\)
c) h1+\(\frac {u_1^2}{2}\)=h2+\(\frac {u_2^2}{2}\)
d) ∇.v=0
View Answer
Explanation: The normal shock wave analysis has the basic equations which are the continuity equation ρ1u1=ρ2u2, momentum equation p1+ρ1u\(_1^2\)=p2+ρ2u\(_2^2\) and the energy equation h1+\(\frac {u_1^2}{2}\)=h2+\(\frac {u_2^2}{2}\). The equation ∇.v=0 is the incompressible flow equation for a steady flow. The normal shock wave is a compressible flow.
6. The most important quantity that dominates the physical properties of compressible flow is _______
a) Speed of sound
b) Speed of light
c) Density of medium of propagation
d) Distance of propagation
View Answer
Explanation: The speed of sound is the quantity that dominates the physical properties of compressible flow. Speed of light is not important in compressible flow problems. Density of medium and distance of propagation are secondary quantities.
7. The equation a=-ρ\(\frac {da}{d\rho }\) where a is the speed of sound in the medium is the mathematical expression derived for the sound waves, which are _________
a) Isentropic
b) Incompressible
c) Adiabatic
d) Reversible
View Answer
Explanation: The equation a=-ρ\(\frac {da}{d\rho }\) is the equation for the speed of sound in the medium. This is derived from the governing equations for sound waves, which are isentropic (adiabatic and reversible). Sound waves may or may not be compressible.
8. The fundamental expression for the speed of sound in a gas is not given by which of the following equations?
a) a2=\(\frac {dp}{d\rho }\)
b) a=\(\sqrt {(\frac {\partial p}{\partial \rho })s}\)
c) a=\(\sqrt {\frac {\gamma p}{\rho }}\)
d) a=\(\sqrt {\gamma ^2RT}\)
View Answer
Explanation: The flow through the sound wave is isentropic, giving a=-ρ\(\frac {da}{d\rho }\). Also, a2=\(\frac {dp}{d\rho }\) and since the change is isentropic, subscript sis used i.e. a=\(\sqrt {(\frac {\partial p}{\partial \rho })_s}\). Moreover, using the isentropic relations for pressure and density we get a=\(\sqrt {\frac {\gamma p}{\rho }}\) and by using the equation of state, we get the temperature relation with the speed of sound in medium i.e. a=\(\sqrt {\gamma RT}\).
9. The speed of sound in any medium is a function of_____
a) P, ρ
b) P, T
c) T only
d) T, ρ
View Answer
Explanation: The speed of sound in any given medium is expressed generally using the equations involving pressure and density (P, ρ). But using the isentropic relations and the gas equation we can simplify it to show that speed of sound in any medium is a function of temperature only a=\(\sqrt {\gamma RT}\).
10. The isentropic compressibility, in terms of speed of sound in any medium is given by ________
a) τs=ρa2
b) τs=\(\frac {1}{\rho a^2}\)
c) τs=\(\frac {\rho }{a^2}\)
d) τs=\(\frac {1}{\rho a}\)
View Answer
Explanation: The speed of sound in any medium is given by a2=\(\frac {dp}{d\rho }\) and the isentropic compressibility is related to the speed of sound as τs=\(\frac {1}{\rho a^2}\). To derive this, v=\(\frac {1}{\rho }\) has been used. The higher is the compressibility, the lower the speed of sound.
11. Select the incorrect statement out of the following.
a) limτs→0 is the case of an incompressible flow
b) Speed of sound in incompressible medium is zero
c) Mach number for finite velocity object, in incompressible flow is zero
d) Incompressible flow is theoretically zero-Mach number flows
View Answer
Explanation: Incompressible flow is the limiting case of isentropic compressibility being zero. This gives an infinite speed of sound and a zero Mach number in that medium. Thus, theoretically, zero-Mach number flows are incompressible.
12. Mach number is a measure of the directed motion of the gas compared with the random thermal motion of the molecules.
a) False
b) True
View Answer
Explanation: This comes from the physical meaning of the Mach number. When we take the ratios of per unit mass kinetic energy to the potential energy of the fluid particle moving along a streamline, it comes proportional to the square of the Mach number. Thus, this is true.
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Aerospace Engineering Books
- Practice Aerospace Engineering MCQs
- Check Aerodynamics Books
- Apply for Aerospace Engineering Internship
- Practice Aeronautical Engineering MCQs
