This set of Aerodynamics Interview Questions and Answers for freshers focuses on “Nonlifting Flow over Cylinder”.
1. A combination of uniform flow and doublet flow gives ______________
a) flow past a circular cylinder
b) flow past a wedge
c) flow past a plate
d) flow over any body
View Answer
Explanation:
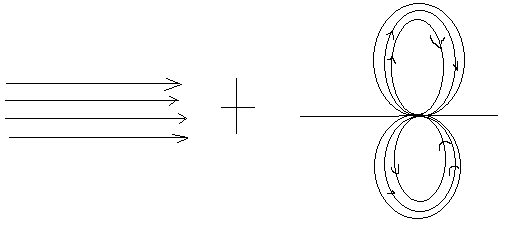
In the above figure, the first diagram shows the uniform flow whereas, the second one shows the doublet flow (source sink combination of equal strength). The combination of these two leads to the flow past a cylinder.
2. The stream function can be obtained by _______
a) sum of stream function of uniform flow and doublet flow
b) difference of stream function of uniform flow and doublet flow
c) sum of stream function of uniform flow and source flow
d) sum of stream function of uniform flow and sink flow
View Answer
Explanation: The stream for the resultant flow can be given by the sum of stream function of uniform flow and doublet flow. Here we need to consider cylindrical coordinates. Mathematically,
Ψ = U*y + ((-u/2*pi*r)*sin θ.
3. The flow past cylinder is also called as _________
a) Vortex flow
b) Source flow
c) Rankine oval of equal axes
d) Newton’s ring
View Answer
Explanation: The flow past cylinder is called a Rankine oval of equal axes as it was discovered by Rankine and also the flow parameters on the upper and lower surface of the doublet flow remains the same.
4. The shape of Rankine oval of equal axes can be found out by substituting ______________
a) Ψ=0
b) Ψ=1
c) U=0
d) U=1
View Answer
Explanation: The shape of the Rankine oval of equal axes can be given by substituting the stream function as zero in the equation Ψ = U*y + ((-u/2*pi*r)*sin θ. This gives us two different solutions for which the shape of oval varies.
5. What will be the shape of Rankine oval when sin θ=0?
a) vertical line
b) horizontal line
c) a point
d) curve
View Answer
Explanation: The shape of the Rankine oval of equal axes can be given by substituting the stream function as zero in the equation Ψ = U*y + ((-u/2*pi*r)*sin θ. When sin θ=0, θ=0, then a horizontal line through the origin of the doublet is formed and it is x-axis.
6. What will be the shape of Rankine oval when U*y+ ((-u/2*pi*r) = 0?
a) open curve
b) closed body profile
c) straight line
d) point
View Answer
Explanation: The shape of the Rankine oval of equal axes can be given by substituting the stream function as zero in the equation Ψ = U*y + ((-u/2*pi*r)*sin θ. When U*y+ ((-u/2*pi*r) =0, a closed profile body is a circular cylinder of radius R with the centre on the doublet.
7. The amount of lift generated in the flow over a cylinder is __________
a) Infinity
b) Positive lift
c) Negative lift
d) No lift
View Answer
Explanation: The pressure distribution over the top of the cylinder is exactly balanced the lower of the cylinder and also, the pressure distribution over the front of the cylinder is balanced by the pressure over the back of the cylinder and hence no lift is generated.
8. In real life, zero drag is acceptable.
a) True
b) False
View Answer
Explanation: In real life, zero drag is not acceptable because we know that drag is produced due to viscous effects which generate frictional shear stress at the body surface and which cause the flow to separate from the surface on the back of the body and thus large wake downstream is created destroying the symmetry of the flow.
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Aeronautical Engineering MCQs
- Check Aeronautical Engineering Books
- Apply for Aerospace Engineering Internship
- Check Aerodynamics Books
- Practice Aerospace Engineering MCQs
