This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Application to Supersonic Airfoils”.
1. Which of these equations is used for computing the lift and wave drag over a supersonic airfoil?
a) Cp=\(\frac {2θ}{\sqrt {M_∞^2-1}}\)
b) Cp=\(\frac {2θ}{\sqrt {M_∞^2+1}}\)
c) Cp=\(\frac {\sqrt {M_∞^2-1}}{θ}\)
d) Cp=\(\frac {\sqrt {M_∞^2+1}}{θ}\)
View Answer
Explanation: Cp=\(\frac {2θ}{\sqrt {M_∞^2-1}}\) is the formula which is known as linearized supersonic pressure coefficient.
Where, θ is the angle made by surface relative to the horizontal. This value is very small
M∞ is the free stream mach number.
This formula is applicable for slender 2-dimensional body and can be used to for estimating the value of both lift and wave drag for supersonic airfoils.
2. What is the value of Cp at the forward surface in a biconvex airfoil?
a) Zero
b) Positive
c) Negative
d) Infinite
View Answer
Explanation: When there is freestream flow towards a biconvex supersonic thin airfoil, using linearlized theory, the sign conventions states positive value of Cp for the forward surface. The surface is inclined into the free stream velocity.
3. The Cp value for supersonic airfoil surface which is inclined away from the freestream is positive.
a) True
b) False
View Answer
Explanation: According to the sign conventions of the linearized theory, for a supersonic biconvex airfoil, if the airfoil surface is inclined away from the freestream velocity, then the value of coefficient of pressure is negative. This the rearward portion of the airfoil has a negative Cp value.
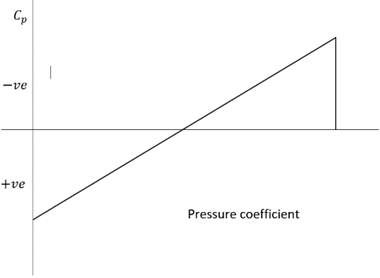
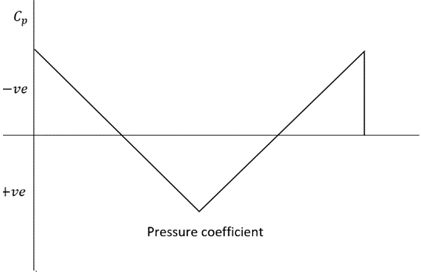
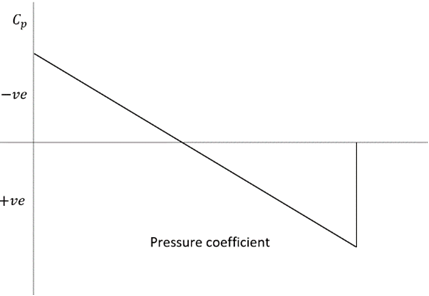
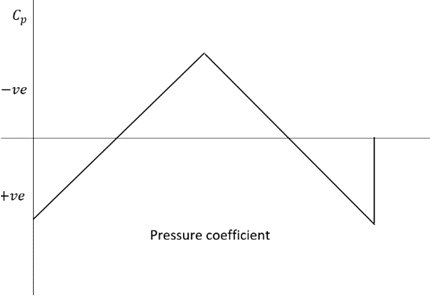
4. Which of these graphs represent the variation of Cp over a biconvex airfoil?
a)
b)
c)
d)
View Answer
Explanation: According to linearized supersonic surface pressure the coefficient of pressure for the forward surface of the biconvex airfoil or any slender two-dimensional shaped airfoil is positive. Whereas the rear surface of the airfoil has a negative coefficient of pressure.
5. According to lineralized theory, what is the formula for coefficient of lift over the a flat plate in a supersonic flow?
a) cl=\(\frac {4α}{\sqrt {M_∞^2-1}}\)
b) cl=\(\frac {4α^2}{\sqrt {M_∞^2-1}}\)
c) cl=\(\frac {4α}{\sqrt {M_∞^2+1}}\)
d) cl=\(\frac {4α^2}{\sqrt {M_∞^2+1}}\)
View Answer
Explanation: Using linearlized theory, we can calculate the lift over a flat plate in supersonic flow. This is done by first calculating the the pressure over the upper and the lower surface.
cp,l=\(\frac {2α}{\sqrt {M_∞^2-1}}\)
cp,u=\(\frac {-2α}{M_∞^2-1}\)
The upper surface is inclined away from the free stream thus it has a negative value.
The normal and axial forces are computed as follows:
cn=\(\frac {1}{c} \int _0^c\) (cp,l-cp,u)dx=\(\frac {1}{c} \int _0^c \big ( \frac {2α}{\sqrt {M_∞^2-1}}-\frac {-2α}{\sqrt {M_∞^2-1}} \big ) \)dx
cn=\(\frac {4α}{\sqrt {M_∞^2-1}}\)
Similarly,
ca=\(\frac {1}{c} \int _{LE}^{TE}\)(cp,u-cp,l)dy=0
The value above is zero because for a thin plate of negligible thickness, dy=0.
Substituting the normal and axial forces in coefficient of lift formula:
cl=cncosα-casin∝=cn-ca∝
This is because the value of ∝ is very very small resulting in cosα~1,sinα~α.
cl=\(\frac {4α}{\sqrt {M_∞^2-1}}\)
6. Wave drag coefficient as derived from linearized theory is independent of the airfoil shape and thickness.
a) True
b) False
View Answer
Explanation: The wave drag as derived from linearized theory is not independent of the airfoil shape. As per the formula given below, it is dependent on gc and gt which are a function of airfoil’s camber and thickness.
cd=\(\frac {4(α^2+g_c^2+g_t^2)}{\sqrt {M_∞^2-1}}\)
7. What is the lift coefficient over a flat plate at an angle of attack of 3 degrees in a supersonic flow at Mach 4?
a) 0.0512
b) 0.0541
c) 0.0628
d) 0.0714
View Answer
Explanation: Given, α=3 deg=0.05236 rad, M=4
The lift coeeficient formula according to the linearized theory is :
cl=\(\frac {4α}{\sqrt {M_∞^2-1}}\)
Substituting the values:
cl=\(\frac {4 × 0.05236}{\sqrt {4^2-1}}\)=0.0541
8. For supersonic flow, which differential equation is obtained for the linearized perturbation potential equation?
a) Elliptic partial differential equation
b) Hyperbolic differential equation
c) Parabolic differential equation
d) Linear differential equation
View Answer
Explanation: The linearized perturation potential equation is given by:
1-M\(_∞^2=\frac {∂^2 \hat {ϕ}}{∂x^2}+\frac {∂^2 \hat {ϕ}}{∂y^2}\)=0
Where, \(\hat {ϕ}\) is ther perturbation potential
M∞ is the free stream Mach number
In case of supersonic flow, 1-M\(_∞^2\) < 0 since Mach number is greater than 1. For this case the equation becomes hyperbolic differential equation which is of the type \( \frac {∂^2 u}{∂x^2}+\frac {∂^2 u}{∂y^2}\).
9. What happens to the coefficient of pressure in a supersonic flow for an increase in Mach number?
a) Increases
b) Decreases
c) Remains unaffected
d) First increases then decreases
View Answer
Explanation: For linearized supersonic flow, the coefficient of pressure is inversely proportional to \(\sqrt {M_∞^2-1}\). Thus, when the Mach number increases, the coefficient of pressure decreases. This in contrast to the trend followed by the subsonic flow where an increasing Mach number results in decreasing coefficient of pressure.
10. What is the source of wave drag exerted on the supersonic airfoil?
a) Shock waves
b) Skin friction
c) Viscous boundary layer
d) Trailing vortex
View Answer
Explanation: Wave drag is a result of pressure distribution which is exerted over the airfoil. This is a consequence of formation of shock waves and expansion wave pattern due to the presence of supersonic flow.
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Aerodynamics Books
- Practice Aerospace Engineering MCQs
- Apply for Aerospace Engineering Internship
- Check Aeronautical Engineering Books
- Check Aerospace Engineering Books
