This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Couette Flow”.
1. What is an assumption made while considering Couette flow?
a) Flow is unparallel
b) No slip condition between two plates
c) Flow is inviscid
d) Both the plates are stationary
View Answer
Explanation: In analyzing Coutte flow, we have two flat plates kept parallel to each other with viscous fluid contained between the two. One major assumption made is that there is a no slip condition thus resulting in no relative motion between the fluid and the plate.
2. The two plate in Couette flow are kept at the same temperature.
a) True
b) False
View Answer
Explanation: To model the Couette flow, the two flat plates are kept at different temperatures. This causes a temperature gradient in the flow. This leads to the transfer of heat energy through the fluid. The heat transfer on the upper and lower plates are given by \(\dot {q}_e\) and \(\dot {q}_w\) respectively.
3. Which of these phenomena results in viscous dissipation?
a) Kinetic energy transformed into internal energy
b) Acceleration of flow
c) Temperature gradient
d) Hot wall and cold wall case
View Answer
Explanation: The flow has kinetic energy which is partially dissipated in the form of internal energy due to the presence of skin friction drag that exists between the fluid and the flat plate. The change in internal energy leads to change in dissipation. These particular phenomena are known as viscous dissipation.
4. What is a cold wall case?
a) Heat flowing from fluid to wall
b) Heat flowing from wall to fluid
c) Reducing temperature of upper wall
d) Reducing temperature of lower wall
View Answer
Explanation: The two flat plates in case of a Couette flow is kept at different temperatures thus creating a temperature gradient. This results to heat transfer through the fluid at both upper and lower surfaces of the plate. When the heat flows from fluid to the wall it is known as cold wall case, and when the heat flows from the wall to the fluid, it is known as hot wall case.
5. Which of these laws is used to find the heat flux at a point in the fluid?
a) Fourier law
b) Fick’s law
c) Newton’s law
d) Kepler’s law
View Answer
Explanation: Fourier law which is also known as the law of heat conduction is used to find out the heat flux at any point in the fluid. It is given by the formula:
\(\dot {q}_y\) = – k\(\frac {∂T}{∂y}\)
Where, heat flux is in the y – direction
Minus sign indicates that the heat flows from high temperature to low temperature and thus \(\dot {q}_y\) is in opposite direction to the temperature gradient.
6. Couette flow is a constant pressure flow.
a) True
b) False
View Answer
Explanation: According to the Naver – Stokes equation, the y – momentum for Couette flow is given by:
\(\frac {∂p}{∂y}\) = 0
From this equation, it is evident that the variation of pressure in y – direction is zero. Hence, pressure in Couette flow is constant.
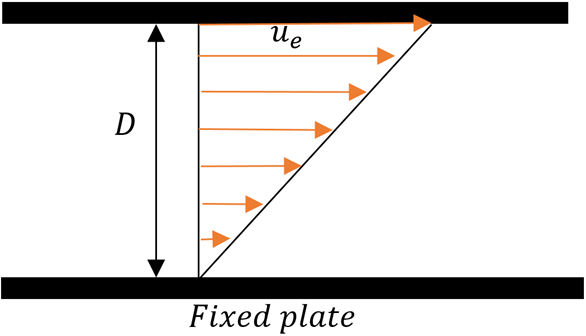
7. How does the velocity vary in case of incompressible Couette flow?
a) Linear
b) Parabolic
c) No variation
d) Hyperbolic
View Answer
Explanation: The velocity variation for an incompressible Couette flow is given by:
u = ue (\(\frac {y}{D}\))
Where, ue is the velocity at y = D that is at the upper plate.
According to the formula, the flow varies linearly across the flow field.
8. What happens to the shear stress if the thickness between the two plates is increased in a Couette flow?
a) Increases
b) Decreases
c) Remains same
d) Becomes infinite
View Answer
Explanation: The relation between the shear stress and the viscous shear layer is given by:
τ = μ(\(\frac {u_e}{D}\))
Where, ue is the velocity at y = D that is at the upper plate.
τ is the shear stress
D is the thickness of the vicsous shear layer/distance between the two parallel plates
As peer the formula, then the thickness of the viscous shear layer increases, the shear stress decreases provided the other properties remain the same.
9. Which of these laws is obeyed by a Newtonian fluid?
a) Shear stress law
b) Newtonian law
c) Incompressible fluid law
d) Prandtl law
View Answer
Explanation: Newtonian fluids are characterized by those fluids that obey the shear stress law. Aeronautics domain makes use of newtonian fluids only (air, other gases). Those fluids that don’t obey shear stress law are known as non – newtonian fluids (blood).
The shear stress law is given by:
τ = μ(\(\frac {∂u}{∂y}\))
This formula helps in obtaining the shear stress at any point in the fluid flow.
10. Where does the maximum value of the temperature occurs in a Couette flow?
a) Top plate
b) Bottom plate
c) Midpoint between the two plates
d) No maximum temperature occurs
View Answer
Explanation: The temperature variation in the Couette flow is given by:
T = Tw + \(\frac {Pru_e^2}{2c_p} \big [\frac {y}{D} – \big ( \frac {y}{D} \big )^2 \big ] \)
Where, Tw is the temperature at y = 0 that is at the lower plate
ue is the velocity at y = D that is at the upper plate.
Pr is Prandtl number
cp is coefficient of pressure
D is the distance between the two plates
According to this, the temperature in Couette flow varies parabolically in y – direction. The maximum temperature occurs at y = D/2 which is the midpoint between the two parallel plates.
Tmax = Tw + \(\frac {Pru_e^2}{8c_p}\)
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Aerospace Engineering MCQs
- Check Aerodynamics Books
- Apply for Aerospace Engineering Internship
- Check Aeronautical Engineering Books
- Check Aerospace Engineering Books
