This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Governing Equations”.
1. What causes the flow properties to vary in quasi – one – dimensional flow?
a) Cross – sectional area
b) Normal shock
c) Head addition
d) Frictional drag
View Answer
Explanation: In case of quasi – one dimensional flow the flow properties keep changing along the distance x due to the varying cross – sectional area (A) which is in contrast to the one – dimensional flow. In that, the area remains constant thus, the flow properties change fir to the presence of shock wave friction and heat addition or removal.
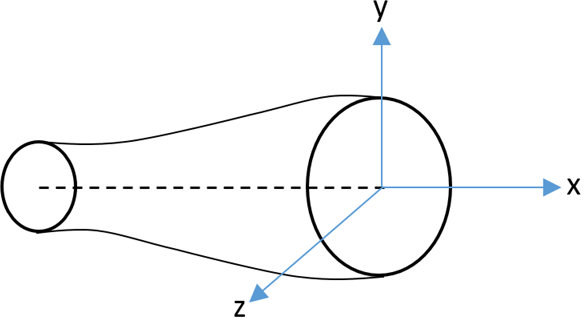
2. What is the momentum equation for a quasi – one dimensional flow?
a) p1A1 + ρ1u\(_1^2\)A1 + \(\int_{A_1}^{A_2}\)pdA = p2A2 + ρ2u\(_2^2\)A2
b) p1A1u1+ ρ1u\(_1^2\)A1 + \(\int_{A_1}^{A_2}\)pdA = p2A2u2+ ρ2u\(_2^2\)A2
c) p1A1 + ρ1u\(_1^2\)A1 = p2A2 + ρ2u\(_2^2\)A2
d) p1A1u1+ ρ1u\(_1^2\)A1 = p2A2u2+ ρ2u\(_2^2\)A2
View Answer
Explanation: The integral form of the momentum equation is given by:
∯S(ρV.dS)V = -∯SpdS
In order to find the x – component of this the equation becomes:
∯S(ρV.dS)u = -∯SpdSx
Where, pdSx is the x component of pressure
u is the velocity
On the control surfaces of the streamtube, V.dS = 0 because they are streamlines. At 1, A1, V, dS are in opposite direction thus they are negative. This results in the left side of the equation to be – ρ1u\(_1^2\)A1 + ρ2u\(_2^2\)A2.
For the right side of the equation, it is –(-p1A1 + p2A2). Negative sign is because at A1, dS points to the left and is negative.
For the upper and lower surfaces of the control volume, pressure integral becomes:
– \(\int_{A_1}^{A_2}\) – pdA = \(\int_{A_1}^{A_2}\)pdA
Where the negative sign is because the dS points to the left.
This results In the equation to be:
– ρ1u\(_1^2\)A1 + ρ2u\(_2^2\)A2 = -(-p1A1 + p2A2 ) + \(\int_{A_1}^{A_2}\)pdA
On rearranging the terms we get:
p1A1 + ρ1u\(_1^2\)A1 + \(\int_{A_1}^{A_2}\)pdA = p2A2 + ρ2u\(_2^2\)A2
3. Which is the Euler’s equation for the quasi – one dimensional flow?
a) dp = \(\frac {ρ}{u}\)du
b) dp = –\(\frac {u}{ρ}\)du
c) dp = -ρudu
d) dp = ρudu
View Answer
Explanation: We consider a duct of variable cross sectional area with two stations 1 and 2, having properties as given in the figure.
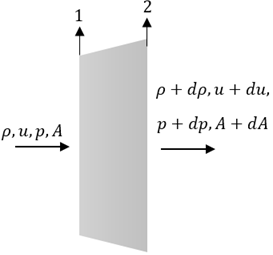
Using the momentum equation:
p1A1 + ρ1u\(_1^2\)A1 + \(\int_{A_1}^{A_2}\)pdA = p2A2 + ρ2u\(_2^2\)A2
We get,
pA + ρu2A + pdA = (p + dp)(A + dA) + (ρ + dρ)(u + du)2 (A + dA)
pA + ρu2A + pdA = pA + pdA + Adp + dpdA + ρu2 + (ρdu2 + 2ρudu + dρu2 + dρdu2 + 2dρudu)(A + dA)
Since the conditions at station 1 are: p, ρ, A and conditions at station 2 are (p + dp), (ρ + dρ), (A + dA).
The product of differentials dPdA, dρ(du)2(A + dA) are negligible thus are ignored.
The resulting equation is:
AdP + Adρu2 + ρu2dA + 2ρuAdu = 0 ➔ eqn 1
The continuity equation is given by:
d(uρA) = 0
Expanding this we get,
ρudA + ρAdu + Audρ = 0
Multiplying the above equation by u on both sides we get:
ρu2dA + ρuAdu + Au2dρ = 0 ➔ eqn 2
Subtracting eqn 2 from eqn 1, we get the differential equation for the quasi one – dimensional flow:
dp = -ρudu
4. What is the differential form of momentum equation for the quasi one – dimensional flow known as?
a) Froude equation
b) Euler’s equation
c) Kelvin’s equation
d) Bernoulli’s equation
View Answer
Explanation: The differential form of momentum equation for the quasi one – dimensional flow is given by:
dp = – ρudu
This is known as Euler’s equation which is derived from the momentum equation.
5. What is the differential form of energy equation for quasi one – dimensional flow?
a) dh – u2du = 0
b) dh – udu = 0
c) dh + u2du = 0
d) dh + udu = 0
View Answer
Explanation: The energy equation for quasi one – dimensional flow is given by:
h + \(\frac {u^2}{2}\) = constant
On differentiating the above equation we arrive at the differential energy equation for the quasi one – dimensional flow:
dh + udu = 0
6. What is the value of surface integral between surface 1 and 2 of the control volume while finding the continuity equation?
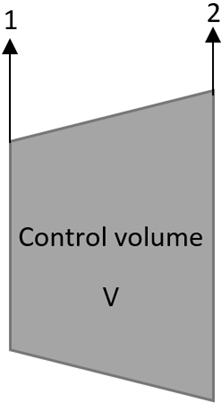
a) V.dS
b) dS
c) Zero
d) V2.dS
View Answer
Explanation: The continuity equation for quasi one – dimensional flow is obtained by integrating conservative equation in a control volume which is given by:
ρ1u1A1 = ρ2u2A2
Where subscript 1 and 2 correspond to the cross – sectional area in the control volume. The surface integral between 1 and 2 is considered to be zero as V is along the surface of the streamtube and hence V.dS = 0 and there is no fluid flow across the boundary of the stream tube.
7. According to the energy equation, which of these properties remain constant along the flow?
a) Total enthalpy
b) Total entropy
c) Kinetic energy
d) Potential energy
View Answer
Explanation: The energy equation stated for steady quasi – one – dimensional flow is given by h1 + \(\frac {u_1^2}{2}\) = h2 + \(\frac {u_2^2}{2}\). According to this formula which is derived for the adiabatic flow, the total enthalpy remains constant (h0 = 0).
8. The governing equations for quasi – one – dimensional flow is used to find properties of flow in a nozzle.
a) True
b) False
View Answer
Explanation: The three governing equations for quasi – one – dimensional flow is used to compute properties such as pressure, enthalpy, density of a flow inside a nozzle or a diffuser. Apart from this the area – velocity relation also helps in understanding the physics of supersonic/subsonic flow.
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Aerospace Engineering Books
- Check Aeronautical Engineering Books
- Practice Aeronautical Engineering MCQs
- Practice Aerospace Engineering MCQs
- Apply for Aerospace Engineering Internship
