This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Supersonic Nozzle Design”.
1. What should be the shape of the nozzle to achieve supersonic speed?
a) Convergent
b) Divergent
c) Convergent-Divergent
d) Divergent-Convergent
View Answer
Explanation: In order to achieve supersonic speed from rest we use a convergent divergent nozzle. This is because in the convergent section the flow is subsonic and is accelerated with decreasing cross-sectional area of the nozzle. The flow reaches sonic speed at the throat after which it is further accelerated in the divergent section as the supersonic flow increases with the increasing cross-sectional area of the nozzle.
2. What is the shortcoming of analysing flow properties using quasi-one-dimensional analysis?
a) Time consuming
b) Inaccurate
c) No information on wall contours of nozzle
d) Unable to predict all the flow properties
View Answer
Explanation: Flow properties at any section of the nozzle can be predicted by the quasi-one-dimensional analysis. It represents the average flow quantities. There are two major shortcomings of using this analysis. First being that it does not predict the three-dimensional flow in convergent-divergent nozzle and secondly, it does not provide us with the information of wall contours in the nozzle.
3. What is the portion of the nozzle called where the angle between the tangent to the wall and horizontal decreases?
a) Divergent section
b) Expansion section
c) Straightening section
d) Convergen section
View Answer
Explanation: When we see the nozzle contour, there are two sections. One where the angle θ which is the angle formed between the tangent to the wall and horizontal increases until it reaches a maximum point. After this, θ reduces until it is equal to zero at the nozzle exit. This section is known as straightening section.
4. Characteristic lines are those lines in the flow field where the flow variables cannot be determined.
a) True
b) False
View Answer
Explanation: There exists some lines in a flow field where the derivatives of the flow variables are indeterminate. For example, along the flow if we assume that there’s a point P, there will be a line along this point where \(\frac {∂^2 ϕ}{∂x∂y}\) is indeterminate as it takes 0/0 form. This line is known as the characteristic line.
5. How many characteristic line/lines can pass through a point P in a streamline?
a) 1
b) 2
c) 3
d) 4
View Answer
Explanation: For a point in a streamline, there exists two characteristic liens according to this formula:
\((\frac {dy}{dx})\)char = tan(θ ± μ)
Where, θ is the angle made between the tangent to the point P and horizontal
μ is local Mach angle = sin-1(1/M)
Thus the two characteristic lines have slope tan(θ + μ) and tan(θ – μ). The one which is inclined above the streamline is labelled as C+ and the characteristic line inclined below the streamline is C–.
6. Which of these steps is not involved in method of characteristics for supersonic nozzle design?
a) Determining characteristic lines
b) Determining compatibility equations for characteristic line
c) Solving compatibility equation point by point
d) Neglect the internal points
View Answer
Explanation: The method of characteristic is a three step procedure. The first step is to determine the characteristic lines. After this, we determine the compatibility equations based on whether the point is an internal or wall point, and finally, we solve for these equations point by point along the characteristic line.
7. What is the proses of applying method of characteristic known as?
a) Unit process
b) Numerical process
c) Characteristics formulation
d) Computation process
View Answer
Explanation: In order to design a supersonic nozzle, it is important to apply methods of characteristics which helps us in determining the flow properties. Solving the compatibility equation point by point along the characteristic line based on whether the internal or wall point is known as unit process.
8. At which point is the initial data taken for nozzle flow?
a) Downstream of the limiting characteristic
b) Upstream of the limiting characteristic
c) Expansion region
d) Straightening section
View Answer
Explanation: For solving method of characteristic, it is important to choose an initial point where the flow field properties are known. The method os characteristic can thus be used to find the flow downstream point by point. For nozzle flor or internal flow, the initial point is taken downstream of the limiting characteristic which is approximately slightly downstream of the sonic line.
9. Lines originating after limiting line intersect the sonic line.
a) True
b) False
View Answer
Explanation: Limiting line is defined as the line in the nozzle beyond which any characteristic line originating downstream does not intersect the sonic line. On the other hand, any line originating between the sonic line and the limiting line will intersect the sonic line.
10. If we know the location and flow properties of internal points 1 and 2, then what is the value of local streamline direction θ3 for point 3 which lies at the intersection of characteristic lines?
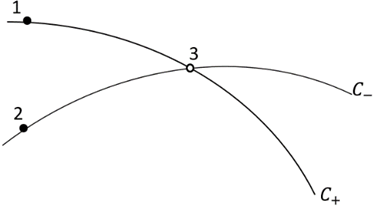
a) θ3 = \(\frac {1}{2}\)[(K–)1 + (K+)2]
b) θ3 = [(K–)1 + (K+)2 ]
c) θ3 = \(\frac {1}{2}\)[(K–)1 – (K+)2]
d) θ3 = [(K–)1 – (K+)2]
View Answer
Explanation: For internal point 1 and 2 having characteristic lines C+ and C– respectively, we know the flow properties. To derive the flow properties of point 3 which lies at the intersection point of the two characteristic lines, we know that K– value is constant onver a characteristic line.
Thus, K–1 = K–3 = θ1 + ν1 since it lies along the same characteristic line C+. Similarly, K+2 = K+3 = θ2 – ν2 because point 3 and 2 lie along the same characteristic line C–.
Solving for the following equation:
K–3 = θ1 + ν1
K+3 = θ2 – ν2
We get,
θ3 = \(\frac {1}{2}\)[(K–)1 + (K+)2]
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Aeronautical Engineering Books
- Apply for Aerospace Engineering Internship
- Check Aerospace Engineering Books
- Practice Aeronautical Engineering MCQs
- Check Aerodynamics Books
