This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Reflected Shock Wave”.
1. What is the velocity behind a reflected shock wave?
a) Equal to the wave velocity
b) Zero
c) Less than the wave velocity
d) More than the wave velocity
View Answer
Explanation: The intensity of this reflected shock (WR) is such that with velocity up, the originally induced mass motion is stopped dead at the wall. The mass motion behind the shock wave that is reflected must be zero. Therefore, the reflected shock wave maintains the zero – velocity boundary state.
2. What is a wave diagram?
a) Plot of wave motion between t and x
b) Plot of reflected wave motion between t and x
c) Diagram of shock creation inside shock tube
d) Plot of wave motion between x and t
View Answer
Explanation: When unsteady wave motion i.e. moving shock wave is studied, wave diagram is often constructed. It is a sketch of the wave diagram plot on a graph with x – axis representing distance and y – axis representing the time. The diagram shows where the incident, reflected shock occurs after applying the boundary conditions.
3. What is the relation between velocity of the wave and reflected shock wave?
a) WR = W
b) WR < W
c) WR > W
d) WR × W = ∞
View Answer
Explanation: On observing the wave diagram it is often seen that for a good reflected shock wave characteristics, the velocity of the reflected shock wave is smaller than the velocity of the wave (WR < W). Thus, in the wave diagram, the slope of the reflected shock wave path is steeper.
4. What is the continuity equation for a reflected shock wave?
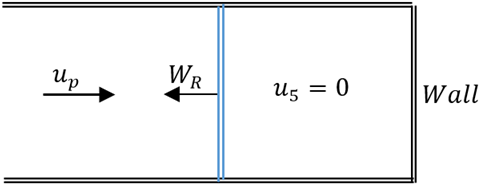
a) ρ1W = ρ5up
b) ρ1W = ρ2(W – up)
c) ρ2(WR + up) = ρ5WR
d) ρ1W = ρ5(W + up)
View Answer
Explanation: Continuity equation across a shock wave is given by the formula
ρ1u1 = ρ2u2
Where, subscripts 1 and 2 are the sections behind and ahead of the shock wave. This above formula is valid only for stationary wave. For a reflected unsteady shock wave, the velocity ahead of the shock relative to wave is WR + up and the velocity behind the shock relative to the wave is WR. Thus, the continuity equation becomes:
ρ2(WR + up) = ρ5WR
5. If the Mach number of the moving shock wave relative to the laboratory Ms = 1.25 then what is the Mach number of the reflected shock wave in a calorically perfect gas?
a) 1.2331
b) 1.4821
c) 1.5671
d) 1.1102
View Answer
Explanation: Given, Ms = 1.25
The relation between Ms and MR is:
\(\frac {M_R}{M_R ^2 – 1} = \frac {M_s}{M_s ^2 – 1} \sqrt {1 + \frac {2(γ – 1)}{(γ + 1)^2}(M_s^2 – 1)\big (γ + \frac {1}{M_s ^2} \big )}\)
Substituting the values we get
\(\frac {M_R}{M_R ^2 – 1} = \frac {1.25}{1.25^2 – 1}\sqrt {1 + \frac {2(1.4 – 1)}{(1.4 + 1)^2} (1.25^2 – 1)\big (1.4 + \frac {1}{1.25^2} \big )} \)
\(\frac {M_R}{M_R ^2 – 1} = \frac {1.25}{1.25^2 – 1}\sqrt {1 + \frac {2(1.4 – 1)}{(1.4 + 1)^2} (1.25^2 – 1)\big (1.4 + \frac {1}{1.25^2} \big )} \)
\(\frac {M_R}{M_R ^2 – 1}\) = 2.20\(\sqrt {1 + \frac {0.8}{5.76} (0.5625)(2.04)}\) = 2.3689
MR = 2.3689 MR2 – 2.3689MR
On solving the quadratic equation we get two results:
MR = 1.2331, – 0.81
Negative values of Mach number is not possible, hence MR = 1.2331
6. What is the Mach number of the reflected wave if the velocity of the reflected wave is 600 m/s, velocity of induced mass motion is 350 m/s and the speed of air is 400 m/s?
a) 3.5
b) 2.375
c) 1.25
d) 3.561
View Answer
Explanation: Given, WR = 600 \(\frac {m}{s}\), up = 350 \(\frac {m}{s}\), a2 = 400 m/s
The incident shock wave propagates into the gas ahead of it towards the wall with Mach number Ms which is reflected into the gas ahead of it with Mach number MR. This is given by the formula:
MR = \(\frac {W_R + u_p}{a_2}\)
Substituting the values, we get:
MR = \(\frac {600 + 350}{400}\) = 2.375
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Aerospace Engineering Internship
- Practice Aeronautical Engineering MCQs
- Check Aeronautical Engineering Books
- Check Aerospace Engineering Books
- Practice Aerospace Engineering MCQs
