This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Determination of Compatibility Equations”.
1. Which of these represent compatibility equation along C+ characteristic line?
a) dθ = tan(θ – μ)
b) dθ = \(\sqrt {M^2 + 1} \frac {dV}{V}\)
c) dθ = \(\sqrt {M^2 – 1} \frac {dV}{V}\)
d) dθ = tan(θ – μ)\(\frac {dV}{V}\)
View Answer
Explanation: If we set the numerator of the combination of momentum, continuity and energy equation represented by Cramer’s rule as zero, we get
(1 – \(\frac {u^{2}}{a^{2}}\))dudy + (1 – \(\frac {v^{2}}{a^{2}}\))dxdv = 0
On rearranging the terms we get
(1 – \(\frac {v^{2}}{a^{2}}\))dxdv = – (1 – \(\frac {u^{2}}{a^{2}}\))dudy
\(\frac {dv}{du} = \frac { – (1 – \frac {u^{2}}{a^{2}})dy}{(1 – \frac {v^{2}}{a^{2}})dx}\)
Substituting the value of characteristic curve in the above equation –
\(\frac {dy}{dx_{char}} = \frac {- \frac {uv}{a^{2}} ± \sqrt {(\frac {u^2 + v^{2}}{a^{2}} ) – 1}}{1 – \frac {u^{2}}{a^{2}}}\)
We get, \(\frac {dv}{du} = \frac {- (1 – \frac {u^{2}}{a^{2}})}{(1 – \frac {v^{2}}{a^{2} })} \big [ \frac { – \frac {uv}{a^{2}} ± \sqrt {(\frac {u^{2} + v^{2}}{a^{2}} ) – 1}}{1 – \frac {u^{2}}{a^{2}}} \big ] = \frac {\frac {uv}{a^{2}} ∓ \sqrt {(\frac {u^{2} + v^{2}}{a^{2}} ) – 1}}{1 – \frac {v^{2}}{a^{2}}}\)
u and v are the x and y – component of velocity V. u = Vcosθ and v = Vsinθ. On substituting these values we get
\(\frac {d(Vsinθ)}{d(Vcosθ)} = \frac {M^2 cosθsinθ ∓ \sqrt {M^2 – 1} }{1 – M^2 sin^2 θ}\)
dθ = ∓ \(\sqrt {M^2 – 1}\frac {dV}{V}\)
This the characteristic line along the C+ characteristic line is .dθ = + \(\sqrt {M^2 – 1}\frac {dV}{V}\).
2. Which of these represents K+ constant along the C+ characteristic line?
a) θ + ν(M) = const
b) θ – ν(M) = const
c) θ + 2ν(M) = const
d) θ – 2ν(M) = const
View Answer
Explanation: The K+ constant along the C+ characteristic line is obtained by integrating the compatibility equation dθ = ∓\(\sqrt {M^2 – 1}\frac {dV}{V}\). Where, ν(M) is the Prandtl – Meyer function and we obtain the K+ constant as θ + ν(M) = const.
3. K+ and K– constant along the characteristic lines are analogous to the Reimann constants.
a) True
b) False
View Answer
Explanation: K+ and K– constant along the characteristic lines are analogous to the Reimann constants J+ and J– both of which are obtained by integrating the compatibility equations obtained for the unsteady flows.
4. Which of these is not an application of a hodograph?
a) Solution for method of characteristics
b) Obtaining motion of celestial objects
c) Swinging Artwood’s machine
d) Determining temperature
View Answer
Explanation: Hodograph is a velocity diagram which has its applications in finding the graphical solution of the methods of characteristics in high tech computers as it related velocity to characteristic lines, obtaining the position of stars, planets, swinging Artwood’s machine as well as in metrological department.
5. K+ and K– constant along the characteristic lines related velocity to J+ and J– constants.
a) True
b) False
View Answer
Explanation: K+ and K– constants along the characteristic lines are given by:
θ + ν(M) = const (along C+ characteristic line)
θ – ν(M) = const (along C+ characteristic line)
These equations relate the magnitude of velocity with the direction of C+ and C– characteristic lines which is known as a hodograph characteristic. These help in giving us the solution for the methods of characteristics.
6. If we know the value of θ1,ν1 at point 1 and θ2,ν2 in a flow, then what is the flow field condition at an internal point 3 lying at the intersection of characteristic lines passing from points 1 and 2?
a) θ3 = \(\frac {(K_- )_1 + (K_+ )_2}{2}\)
b) θ3 = \(\frac {(K_- )_1 + (K_+ )_3}{2}\)
c) θ3 = \(\frac {(K_+ )_1 + (K_+ )_2 + (K_+ )_3}{2}\)
d) θ3 = \(\frac {(K_- )_1 + (K_- )_2 + (K_- )_3}{2}\)
View Answer
Explanation: The value of K+ is constant along left running Mach wave and K– is constant along right running Mach wave. Point 3 lies at the intersection of characteristic lines passing through point 1 and 2 thus, considering the characteristic curve passing through point 1,
(K–)1 = (K–)3
θ1 + ν1 = θ3 + ν3
θ3 + ν3 = (K–)1 (equation 1)
Similarly along the characteric curve through point 2,
(K+)2 = (K+)3
θ2 – ν2 = θ3 – ν3
θ3 – ν3 = (K+)2 (equation 2)
Solving equation 1 and 2 we get
θ3 = \(\frac {(K_- )_1 + (K_+ )_2}{2}\)
7. If the flow conditions at point 1 near the nozzle wall is given, then what is the flow conditions at point 2 on the wall?
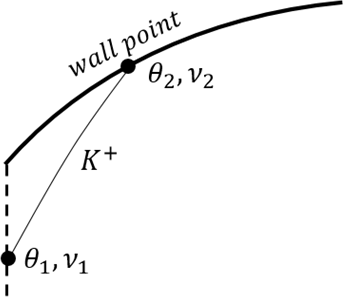
a) ν2 = θ2 + θ1 – ν3
b) ν2 = θ2 – θ1 + ν3
c) ν2 = θ2 – θ1
d) ν2 = θ2 + θ1
View Answer
Explanation: The flow conditions at point 1 is given as θ1,ν1. Since points 1 and 2 lie on the same characteristic line,
(K+)1 = (K+)2
Substituting the values of K+ constant, we get
θ1 + ν1 = θ2 + ν2
ν2 = θ2 – θ1 + ν3
8. Where is methods of characteristics used?
a) Designing supersonic nozzle
b) Designing fuselage’s bulkhead
c) Computing optimum wing camber
d) Designing diamond airfoil for supersonic flow
View Answer
Explanation: Methods of characteristics are used in designing the supersonic nozzle. For this, a line with known supersonic flow fields is required. Upon going downstream, depending on where the point lies (internal/wall) the method of characteristics is applied to find the flow field.
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Aerospace Engineering MCQs
- Apply for Aerospace Engineering Internship
- Practice Aeronautical Engineering MCQs
- Check Aeronautical Engineering Books
- Check Aerospace Engineering Books
