This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Linearized Supersonic Flow”.
1. Which of these is the linearized perturbation velocity potential equation over a thin airfoil in a supersonic flow?
a) λ2(ϕxx + ϕyy) = 0
b) ϕxx + ϕyy = 0
c) λ2ϕxx + ϕyy = 0
d) λ2ϕxx + ϕxy = 0
View Answer
Explanation: For a supersonic flow over a thin airfoil, the two dimensional linearized perturbation velocity potential equation is given by
λ2ϕxx + ϕyy = 0
In this equation the perturbations are assumed to be small with the value of λ = \(\sqrt {M_∞^2 – 1}\).
2. The linearized perturbation velocity potential equation for supersonic flow takes form of which of these partial differential equations?
a) Elliptic
b) Hyperbolic
c) Parabolic
d) Linear
View Answer
Explanation: The linearized perturbation velocity potential equation for supersonic flow differs with the subsonic flow in the type of partial differential equation formed. The equation for supersonic flow given as below which is in the form of hyperbolic partial differential equation.
λ2ϕxx + ϕyy = 0
3. For an airfoil kept at supersonic flow, how does the coefficient of pressure vary with an increase in Mach number?
a) Increases
b) Decreases
c) Remains same
d) First increases, then decreases
View Answer
Explanation: Based on the linearized coefficient of pressure derived for supersonic flow over an airfoil, the coefficient of pressure is inversely proportional to \(\sqrt {M_∞^2 – 1}\). Thus, with an increase in Mach number, the pressure coefficient decreases.
4. What is the coefficient of lift according to the linearized theory over a flat plate kept at an inclination of 4 degrees having freestream Mach number of 3?
a) 0.0987
b) 1.231
c) 0.857
d) 1.362
View Answer
Explanation: Given, M∞ = 3, ∝ = 4 = 0.0698 rad
According to the linearized theory, the coefficient of lift over a flat plate is given by:
cl = \(\frac {4∝}{\sqrt {M_∞^2 – 1}}\)
Substituting the values we get
cl = \(\frac { 4× 0.0698}{\sqrt {9 – 1}} = \frac {0.2792}{2.8284}\)0.0987
5. Linearized equations give the exact results as obtained by the non – linear equations.
a) True
b) False
View Answer
Explanation: The linearized solutions are obtained by taking assumptions in the nonlinear equations to arrive at a closed – form solutions. These assumptions are based on small perturbations and have limitations over the Mach number range.
6. For a biconvex airfoil, what sign convention is used for the value of θ while computing the coefficient of pressure?
a) Positive for forward and negative for rearward surface
b) Positive for upper and negative for lower surface
c) Positive for rearward and negative for forward surface
d) Positive for lower and negative for upper surface
View Answer
Explanation: While computing the pressure coefficient using the linearized equation, there has to be a notation for the sign convention for θ based on its location. For the front end of the biconvex airfoil, θ is positive and for the rearward section, θ is negative. Thus, the coefficient of pressure is positive in the front end and negative at the rear end.
7. For a thin airfoil kept at a supersonic flow of Mach number 3 at an inclination of 2 degrees, what is the coefficient of pressure?
a) 0.47
b) 1.51
c) 1.78
d) 2.83
View Answer
Explanation: Given, M\(_∞^2\) = 3, θ = 2 deg
For the supersonic flow, the linearized coefficient of pressure for small inclinations is given by:
Cp = \(\frac {2θ}{\sqrt {M_∞^2 – 1}}\)
Substituting the values, we get
Cp = \(\frac {2×2}{\sqrt {9 – 1}}\) = 2.83
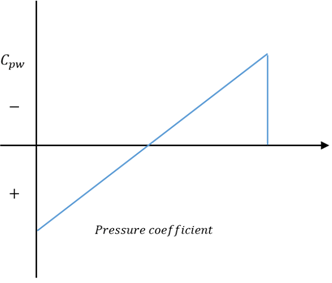
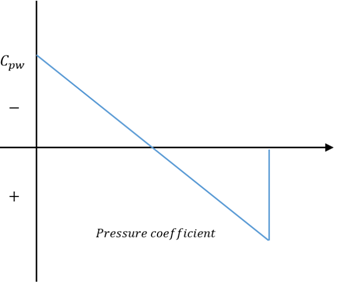
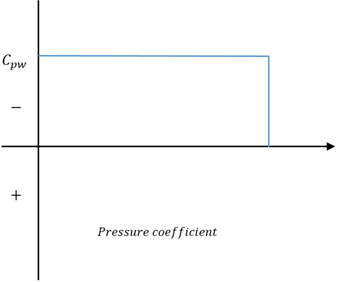
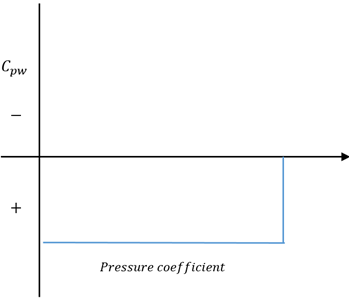
8. Which of these graphs is the correct representation of linearized pressure coefficient over a biconvex airfoil?
a)
b)
c)
d)
View Answer
Explanation: The value of θ is the front end of the biconvex airfoil is positive, whereas at the rearward end, θ is negative. This results in the linearized pressure coefficient to vary from positive to negative as we move from front end to the rear end of the airfoil.
9. Which of these assumptions is not made while formulating the linearized supersonic flow?
a) Thin sharp edged airfoil
b) Large camber
c) Two – dimensional flow
d) Small angle of attack
View Answer
Explanation: Ackeret developed the linearized supersonic theory in which there were simple assumptions made. The airfoil was assumed to be sharp edged, kept at very small angle of attack having small camber in a two – dimensional supersonic flow.
10. The linearized pressure distribution for Mach number greater than 5 matches the coefficient of pressure derived from the exact shock theory.
a) True
b) False
View Answer
Explanation: The coefficient of pressure as obtained from the linearized supersonic theory and the exact oblique shock theory match only until small value of semi angle θ. As the Mach number increases beyond 4, the linearized theory results are not as accurate at the exact oblique shock theory.
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Aerospace Engineering Internship
- Check Aeronautical Engineering Books
- Check Aerospace Engineering Books
- Check Aerodynamics Books
- Practice Aerospace Engineering MCQs
