This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Moving Normal Shock Waves”.
1. What happens when the shock wave propagates in the opposite direction with the same magnitude as wave velocity?
a) Velocity increases
b) Velocity decreases
c) Appears stationary
d) Becomes sonic
View Answer
Explanation: Usually shock waves propagate with subsonic or supersonic speed but when the shockwave propagates in a flow that moves as well, and it is in the opposite direction with the same velocity as the flow, then it appears to be stationary known as ‘standing shock wave’.
2. What happens when normal shock wave propagates into laboratory facility?
a) Induces gas ahead of it
b) Induces gas behind it
c) Leaves a small area of vacuum behind it
d) Leaves a small area of vacuum ahead of it
View Answer
Explanation: When the normal shock wave is not opposed to the flow velocity, it propagates with some velocity W into the laboratory facility. This leads to the induction of gas behind it to move in the wave direction.
3. The flow properties of the moving wave depends on which property/properties?
a) Direction
b) Time
c) Both direction and time
d) Temperature
View Answer
Explanation: Moving shock wave is an example of unsteady flow which means that all its flow properties such as density, velocity, temperature are a function of both the direction (x) and time (t). Although stationary shock wave are steady flow, thus the flow properties are only a function of direction (x).
4. Shock tube is an application of steady motion of the shock waves.
a) True
b) False
View Answer
Explanation: Shock tube makes use of unsteady wave motion. It is a closed tube at both ends having a diaphragm which separates high pressure region known as the driver section and low pressure region known as the driven section.
5. What is the continuity equation for a moving shock wave?
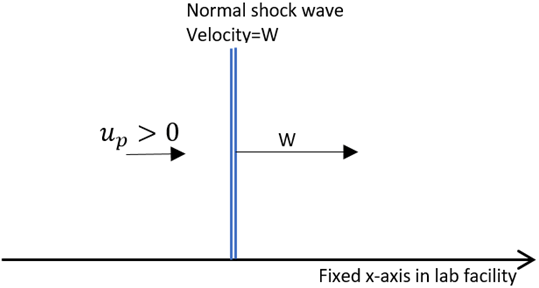
a) ρ1W = ρ2up
b) ρ1W = ρ2(W – up)
c) ρ1(W + up) = ρ2up
d) ρ1W = ρ2(W + up)
View Answer
Explanation: Continuity equation across a shock wave is given by the formula
ρ1u1 = ρ2u2
Where, subscripts 1 and 2 are the sections behind and ahead of the shock wave. The above formula is valid only for stationary wave. For a moving wave, there is a induced gas formation behind the shock wave resulting in (W – up) being the velocity behind the shock wave which is relative to the wave, and W is the velocity of the gas ahead of the shock wave. Thus, the continuity equation becomes:
ρ1W = ρ2(W – up)
up is the velocity of induced mass motion due to the gas
W is the velocity of the normal shock wave.
6. Hugoniot equation is physically dependent on whether the shock wave is stationary or moving.
a) True
b) False
View Answer
Explanation: Hugoniot equation is given by:
e2 – e1 = \( \frac {p_1 + p_2}{2}\)(v1 – v2)
This is derived from the three governing equations – Continuity, momentum and energy equations for a moving shock wave. This equation gives idea of how the thermodynamic variables such as energy, pressure changes across the normal shock wave. It is not dependent on whether the shock wave is stationary or not.
7. Which of these is the governing parameters for change across shock wave when it is moving?
a) Mach number
b) Density
c) Pressure ratio
d) Velocity ratio
View Answer
Explanation: In a stationary wave, changes across the shock wave is governed by the Mach number. But, in a moving shock wave it is dependent majorly on the pressure ratio as seen in the formula below which shows the equation for density and pressure ratio across a moving shock wave.
\( \frac {T_2}{T_1} = \frac {p_2}{p_1} \Bigg ( \frac {\frac {γ + 1}{γ – 1} + \frac {p_2}{p_1}}{1 + \frac {γ + 1}{γ – 1} \frac {p_2}{p_1}} \Bigg )\)
\( \frac {\rho _2}{\rho _1} = \frac {1 + \frac {γ + 1}{γ – 1} \frac {p_2}{p_1}}{\frac {γ + 1}{γ – 1} + \frac {p_2}{p_1}}\)
8. If the wave velocity is 900 m/s and the density ratio across the shock wave is 0.6, then what is the value of velocity of induced mass motion behind the wave?
a) 400 m/s
b) 360 m/s
c) 180 m/s
d) 980 m/s
View Answer
Explanation: Given, W = 900 \( \frac {m}{s}\), \( \frac {\rho _2}{\rho _1}\) = 0.6
For a moving shock wave that propagates into a stagnant gas, it induces a mas motion of velocity up.
This velocity is given by the relation:
up = W\(\big (\)1 – \( \frac {\rho _2}{\rho _1} \big ) \)
Substituting the values:
up = 900(1 – 0.6) = 360 m/s
9. How is total enthalpy related in a stationary shock wave?
a) Constant
b) h2 > h1
c) h2 < h1
d) h02 < h01
View Answer
Explanation: For a stationary shock wave, the total enthalpy remains constant across the shock wave which means that h02 = h01. Although, in case of moving shock wave, this is not the case. The enthalpy does not remain constant across the shock.
10. What is the temperature ratio across a moving shock wave in ambient air if the pressure ratio is 8.5?
a) 1.43
b) 2.37
c) 4.21
d) 3.82
View Answer
Explanation: Given, \(\frac {p_2}{p_1}\) = 8.5, γ = 1.4 (ambient air)
The temperature ratio across a moving shock wave is given by:
\( \frac {T_2}{T_1} = \frac {p_2}{p_1} \Bigg ( \frac {\frac {γ + 1}{γ – 1} + \frac {p_2}{p_1}}{1 + \frac {γ + 1}{γ – 1} \frac {p_2}{p_1}} \Bigg )\)
Substituting the values, we get:
\( \frac {T_2}{T_1}\) = 8.5\( \Bigg ( \frac {\frac {1.4 + 1}{1.4 – 1} + 8.5}{1 + \frac {1.4 + 1}{1.4 – 1} \times 8.5} \Bigg )\) = 8.5\( \Bigg ( \frac {\frac {2.4}{0.4} + 8.5}{1 + \frac {2.4}{0.4} \times 8.5} \Bigg ) \)
\( \frac {T_2}{T_1}\) = 8.5\(\big ( \frac {14.5}{52} \big ) \) = 2.37
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Aeronautical Engineering Books
- Practice Aeronautical Engineering MCQs
- Apply for Aerospace Engineering Internship
- Practice Aerospace Engineering MCQs
- Check Aerodynamics Books
