This set of Aerodynamics Multiple Choice Questions & Answers (MCQs) focuses on “Nozzles”.
1. For a flow in a duct, what is Mach number a function of?
a) Local duct area to sonic throat area
b) Sonic throat area to local duct area
c) Local duct area to convergent duct area
d) Local duct area to divergent duct area
View Answer
Explanation: On observing the area – Mach relation for a flow inside a duct, we notice that the Mach number at a point in a duct is a function of ratio of local duct area to the sonic throat area.
M = f(A/A*)
2. In the area – Mach relation A < A* or A ≥ A*.
a) True
b) False
View Answer
Explanation: In case of area – Mach relation, the value of A can never be less than A* for an isentropic flow because this corresponds to the throat area where Mach number is equal to 1 and has a local minimum area because dA = 0.
3. The area – Mach number relation yields how many solution(s) for a given Mach number?
a) 1
b) 2
c) 3
d) 0
View Answer
Explanation: The area – Mach relation which is the ratio of local area to throat area as a function of Mach number yields two solutions for a given Mach number. One is a subsonic value and the other is the corresponding supersonic value. That value that has to be chosen for a specific Mach number depends on the inlet and exit pressure of the duct.
4. What happens in case of a choked flow?
a) When flow becomes supersonic at the throat
b) When flow is sonic and mass flow remains constant at the throat despite reducing exit pressure
c) When the exit pressure is reduced to a point where the flow becomes subsonic at throat
d) Normal shock is created at the inlet of the nozzle
View Answer
Explanation: When we reduce the exit pressure, there comes a point when the Mach number becomes 1 at the throat i.e. the flow is sonic. The mass flow remains constant and the flow becomes frozen upstream of the throat. This condition where after reaching sonic flow at the throat, and despite reducing the exit pressure, the mass flow remains constant is called choked flow.
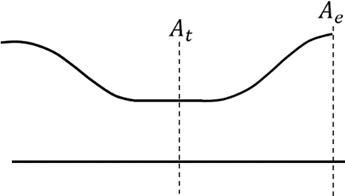
5. For a nozzle with the following data \(\frac {A_e}{A_t}\) = 1.616, P01 = 1 atm, Pe = 0.947 atm, what is the Mach number at the throat of the nozzle?
a) 0.25
b) 0.50
c) 0.75
d) 0.58
View Answer
Explanation: Given, \(\frac {A_e}{A_t}\) = 1.616, P01 = 1 atm, Pe = 0.947 atm
P01 = P0e = 1atm
\(\frac {P_{0e}}{P_e} = \frac {1}{0.947}\) = 1.056
From the isentropic table:
For \(\frac {P_{0e}}{P_e}\) = 1.056, we get Mach number as Me = 0.28
For Me = 0.28, \(\frac {A_e}{A^*}\) = 2.166 (From the gas table)
\(\frac {A_t}{A^*} = \frac {\frac {A_t}{A_e }}{\frac {A^*}{A_e }} = \frac {2.166}{1.616}\) = 1.34
For \(\frac {A_t}{A^*}\) = 1.34, we get Mt = 0.5
6. If the given conditions for a nozzle are P01 = 1 atm, Pe = 0.3143 atm, then what is the ratio of exit area to throat area?
a) 1.15
b) 1.5
c) 1.25
d) 1.115
View Answer
Explanation: Given, P01 = 1 atm, Pe = 0.3143 atm
To calculate – \(\frac {A_e}{A^*}\)
Stagnation pressures remain same P01 = P0e
\(\frac {P_{0e}}{P_e} = \frac {1}{0.3143}\) = 3.182
For \(\frac {P_{0e}}{P_e}\) = 3.182 we get Me = 1.4 (Using gas table)
For Me = 1.4, we get \(\frac {A_e}{A^*}\) = 1.115 (Using gas table)
7. Which of this conditions is necessary to achieve flow in a nozzle?
a) \(\frac {P_e}{P_0}\) < 1
b) \(\frac {P_e}{P_0}\) > 1
c) \(\frac {P_e}{P_0}\) = 1
d) \(\frac {P_e}{P_0}\) = 0
View Answer
Explanation: If the stagnation pressure at the inlet is equal to the exit pressure, then there will be no flow in the nozzle as there is no pressure difference for the flow to move. In order to accelerate the air, the pressure difference has to be created by having pe < p0.
Thus the condition to achieve an accelerated flow inside a nozzle is: \(\frac {P_e}{P_0}\) < 1
8. What is the exit Mach number if the convergent nozzle is choked?
a) 0
b) 1
c) 0.5
d) 1.5
View Answer
Explanation: In case of a convergent nozzle, when the flow is choked the exit Mach number is 1. In order to check if the nozzle is operating at choking conditions, we compare the actual pressure ratio to the critical pressure ratio. When the actual pressure ratio is larger than the critical pressure ratio, the nozzle is considered to be choked.
9. In case of the formation of shock in the divergent section of a C – D nozzle, the flow remains isentropic.
a) True
b) False
View Answer
Explanation: Usually the flow in the nozzle is considered to be adiabatic because there is no heat transfer. But when we try to achieve supersonic flow, there is formation of shock waves. Therefore the region between the throat the exit of the divergent nozzle does not have isentropic flow.
10. What happens to the mass flow rate if the reservoir pressure is doubled?
a) Doubled
b) Remains same
c) Becomes half
d) Becomes one – fourth
View Answer
Explanation: The mass flow rate depends on the inlet stagnation pressure, temperature and throat area by the relation:
\(\dot {m} ∝ \frac {p_0 A^*}{\sqrt {T_0}} \)
Thus, when the resrvoic pressure is doubled, the mass flow rate through the nozzle also doubles as it is directly proportional to it.
11. Which of these conditions result in underexpanded nozzle?
a) Pe = Pa
b) Pe > Pa
c) Pe < Pa
d) Pe << Pa
View Answer
Explanation: In case of underexpanded nozzle, the exit pressure is greater than the ambient pressure Pe > Pa. This leads to formation of expansion wave at the tip of the nozzle and the flow is capable of more expansion.
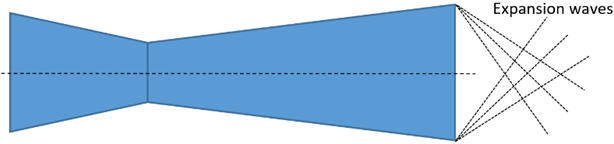
12. In which of these conditions there’s no formation of shock wave inside a convergent – divergent nozzle?
a) Overexpanded
b) Underexpanded
c) Fully expanded
d) Fully underexpanded
View Answer
Explanation: When the nozzle is fully expanded i.e. when the ambient pressure is equal to the exit pressure of the nozzle, there no formation of shock waves. In case of underexpanded nozzle, there are expansion waves formed at the tip of the nozzle exit and in case of overexpanded nozzle, there’s formation of oblique shock waves at the tip.
Sanfoundry Global Education & Learning Series – Aerodynamics.
To practice all areas of Aerodynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Check Aerodynamics Books
- Apply for Aerospace Engineering Internship
- Check Aerospace Engineering Books
- Practice Aerospace Engineering MCQs
- Check Aeronautical Engineering Books
