This set of Nanotechnology Multiple Choice Questions & Answers (MCQs) focuses on “Carbon Nanotubes Structure and Types”.
1. Identify the correct expression for determining the structure of SWCNTs using chiral vector.
a) \(\vec{C_h}\) = n1 â1 + n2 â2
b) \(\vec{C_h}\) = n1 â2 + n2 â1
c) \(\vec{C_h}\) = n1 â1 – n2 â2
d) \(\vec{C_h}\) = n1 â2 – n2 â1
View Answer
Explanation: The mathematical expression of chiral vector is used to specify the structure of SWCNTs.
\(\vec{C_h}\) = n1 â1 + n2 â2
Here, a1 and a2 are unit vectors in the graphene sheet while n1 and n2 are the chiral indices. a1and a2 can be denoted as √(3d) where d is the nearest neighbor C-C distance which is 1.421Å in graphene.
2. What type of notation is shown by zig-zag nanotubes?
a) (n, m)
b) (n, n)
c) (m, n)
d) (n,0)
View Answer
Explanation: CNTs are of various configurations that are zig-zag, armchair and helical. This is dependent on the chirality or the way of folding up of graphene sheets. Zig-Zag nanotubes exhibit (n, 0) indices since m = 0, whereas armchair and helical nanotubes exhibit (n, n) and (n, m) indices respectively.
3. What is the value of chiral angle for armchair configuration of CNTs?
a) θ = 90°
b) θ = 120°
c) θ = 30°
d) θ = 60°
View Answer
Explanation: Chiral angle is defined as the angle between the chiral vector and the zig-zag direction. It is denoted by θ and calculated as θ = tan-1[(√3m)/(m+2n)]. In case of an armchair configuration of carbon nanotubes, θ is necessarily 30° with (n, n) index.
4. Select the correct option with respect to DWCNTs from the given statements.
a) They behave only as metallic material
b) They have lower flexibility than carbon fibers
c) They are resistant to functionalization
d) They have morphology very different from that of SWCNTs
View Answer
Explanation: DWCNTs are double walled carbon nanotubes having morphology and properties similar to SWCNTs. However, DWCNTs are more resistant to chemicals and this is especially significant during their functionalization. These nanotubes are known to have higher flexibility and mechanical strength than carbon fibers. They can have metallic as well as semiconducting properties.
5. What is hybridisation of carbon atoms in CNTs?
a) sp
b) sp2
c) sp3
d) sp2d
View Answer
Explanation: In carbon nanotubes, the carbon atoms are known to form sp2 hybridized bonds, similar to those of graphene. Here there are one 2s orbital and two 2p orbitals. In the tubes one carbon atom is attached to three other carbon atoms while the fourth one remains delocalized in the system.
6. How can one determine the electrical nature of a nanotube?
a) (n+m)/3
b) (n-m)/3
c) (n*m)/3
d) (n÷m)/3
View Answer
Explanation: The structural design of a CNT can affect its electrical nature. If (n-m) is a multiple of 3, that is if (n-m) is completely divisible by 3, then the nanotube is described as a highly conducting metal. However, it is considered as a semiconductor if (n-m) is not a multiple of 3.
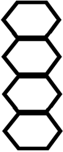
7. The given diagram shows a strip cut out from the circumference of a particular type of CNT. What type of CNT is it?
a) Chiral
b) Zig-zag
c) Helical
d) Armchair
View Answer
Explanation: Strips cut out from the circumference of a zig-zag nanotube appears as shown in the diagram. Indices of zig-zag nanotubes are (n, 0) since m = 0. The chiral vector in this case is θ = 0° and the nanotube can behave either as metallic or semiconducting.
8. Which model describes MWCNTs as “single sheet of graphene rolled in around itself”?
a) Parchment Model
b) Plum pudding model
c) Russian Doll model
d) Rutherford model
View Answer
Explanation: The MWCNTs can be described using two different structural models-the Parchment and the Russian Doll models. The Parchment model describes MWCNTs as a single graphene sheet rolled around itself several times resembling a scroll of parchment or a rolled up newspaper.
9. Define chiral angle.
a) Angle between chiral vector and zig-zag direction
b) Angle between armchair and helical direction
c) Angle between chiral vector and helical direction
d) Angle between zig-zag and armchair direction
View Answer
Explanation: Chiral angle is defined as the angle between the chiral vector \(\vec{C_h}\) and the zig-zag direction. This angle determines the degree of twisting of the CNTs. It is denoted by θ and expressed as:
θ = tan-1[(√3m/2n+m)].
10. Find out the circumference of a nanotube with indices (8, 4).
a) 18.330Å
b) 15.038Å
c) 2.461Å
d) 26.047Å
View Answer
Explanation: The circumference of a nanotube can be denoted as:
c = √3 × dc-c × √(m2+n2+mn)
where dc-c = 1.421Å in graphene and (n, m) = (8, 4) as mentioned in question
∴ c = √3 × 1.421 × 10-10 × √{(82 + 42) + (8 × 4)}
⇒ c = √3 × 1.421 × 10-10 × √112
⇒ c = 26.047 × 10-10 m
⇒ c = 26.047Å
Therefore, circumference of the nanotube is given as c = 26.047Å for the indices (8, 4).
Sanfoundry Global Education & Learning Series – Nanotechnology.
To practice all areas of Nanotechnology, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
