This set of Nanotechnology Multiple Choice Questions & Answers (MCQs) focuses on “Carbon Nanotubes Structure and Types – Set 2”.
1. Carbon nanotubes are cylindrical shaped structures having only close ends.
a) True
b) False
View Answer
Explanation: Carbon nanotubes are very long, cylindrical tubes having diameters typically measured in nanometers. CNTs can have open as well as closed ends. Mostly, CNTs are terminated at both the ends by a pair of hemispherical caps and they are made up of hexagons and pentagons.
2. What would be the diameter of a tube having chiral index of (6, 5)?
a) 16.523Å
b) 7.474Å
c) 21.387Å
d) 13.555Å
View Answer
Explanation: Diameter of a nanotube is obtained as: –
D = c / π = [√3 × dcc × √(m2 + n2 + mn)] / π
D = [√3 × 1.421 × √(62 + 52 + 6 × 5)] / π
D = [√3 × 1.421 × √91] / π
D = 7.474 × 10-10m = 7.474Å.
Hence, diameter of the nanotube is given as D = 7.474Å for the chiral tube (6, 5).
3. What is the dimensionality of carbon nanotubes?
a) 0D
b) 1D
c) 2D
d) 3D
View Answer
Explanation: Carbon nanotubes are allotropes of carbon that have tube like structures with diameters typically in the range of nanometers. These are 1D structures with sp2 hybridization. They are believed to exhibit quantum confinement effect owing to one – dimensional (1D) periodicity.
4. Why are CNTs found to have hemispherical caps?
a) Increase the number of incomplete bonds
b) Reduce the surface area
c) Make it energetically stable
d) Enhance the amount of dangling bonds
View Answer
Explanation: CNTs are generally closed at the ends by a pair of hemispherical caps. These provide a completely closed surface of the tube that has no dangling bonds. This makes the CNTs energetically stable in comparison to the unrolled sheets or open CNTs that have incomplete bonds at its edges.
5. Carbon – nanobuds are created from which two allotropes of carbon?
a) Graphite and Lampblack
b) Diamond and Wood charcoal
c) Gas carbon and Lonsdaleite
d) Carbon nanotubes and Fullerene
View Answer
Explanation: Carbon nanobuds are a newly formed material comprising of single walled carbon nanotubes and fullerenes. In this material the fullerene – like ‘buds’ are covalently bonded on the outer sides of the underlying CNTs.
6. (7, 2) is the chiral index of what kind of nanotube?
a) Achiral
b) Zig – zag
c) Helical
d) Armchair
View Answer
Explanation: The given (n, m) notations correspond to helical configuration. This is because for helical (chiral) nanotubes, the indices should be of the type (n, m) and θ should lie between 0° and 30°. In this case (n, m) = (7, 2) and θ = 12.216°
Here, m = 2, n = 7
∴ θ = tan-1[(√3m / (m + 2n)]
θ = tan-1[(√3 × 2) / {2 + (2 × 7)}]
θ = 12.216°
Thus, it clearly represents an armchair.
7. Choose the incorrect statement with respect to CNTs.
a) They are the strongest and the stiffest fibers
b) They are composed of interlocking carbon atoms.
c) They have extremely high thermal expansion coefficient
d) They have armchair and zig – zag configurations that have high degree of symmetry
View Answer
Explanation: Carbon nanotubes are allotropes of carbon with cylindrical nanostructures. They are the stiffest and strongest fibers that have interlocking carbon atoms. They have several configurations, out of which armchair and zig – zag structures have a high degree of symmetry. However, they have low thermal expansion coefficient but high thermal conductivity.
8. Which of these expressions determine the number of hexagons in a unit cell (N) of a CNT?
a) N = [2 × (m – n)] / dR
b) N = [m2 + n2 – mn] / dR
c) N = [2 × (m2 + n2 + mn)] / dR
d) N = [m2 – 2mn + n2] / dR
View Answer
Explanation: The expression that is used to determine the number of hexagons in a unit cell (N) of a CNT with a chiral index (n, m) is given by:
N = [2 × (m2 + n2 + mn)] / dR
Where dR = d if n – m is not a multiple of 3d
3d if n – m is a multiple of 3d
and d is the greatest common divisor (GCD) of (n, m).
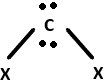
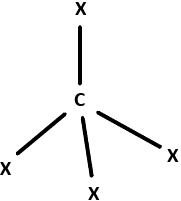
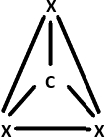
9. Identify the geometry that corresponds to the hybridization of carbon atoms in CNT.
a)
b)
c)
![]()
d)
View Answer
Explanation: Carbon atoms in CNTs exhibit sp2 hybridisation that is a combination of s, px and py orbitals. They form 3σ – bonds with 3 other neighboring carbon atoms while the pz orbitals form the π – bonds and remain delocalized in the system.
10. Which of the following expressions correctly represent the chiral angle of a tube having (n, m) indices?
a) θ = tan-1[(√3m) / (m + 2n)]
b) θ = 276 × √{(n + m)2 – nm}
c) θ = cos (2 / √3) – m / 2
d) θ = √3 × dcc × √(m2 + mn + n2)
View Answer
Explanation: Chiral angle is the angle between the chiral vector and the zig – zag direction. It is described by the following set of equations;
θ = sin-1[(√3 × m) / {2 × √(m2 + n2 + nm)}]
θ = cos-1[(2n + m) / {2 × √(m2 + n2 + nm)}]
θ = tan-1[(√3 × m) / (2n + m)].
Sanfoundry Global Education & Learning Series – Nanotechnology.
To practice all areas of Nanotechnology, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
