This set of Machine Dynamics Question Paper focuses on “Correction Couple to be Applied to Make the Two Mass Systems Dynamically Equivalent”.
1. Correction couple is applied when masses are placed arbitrarily and to maintain _________
a) Static equilibrium
b) Dynamic equilibrium
c) Stable equilibrium
d) Unstable equilibrium
View Answer
Explanation: Difference between the torques required to accelerate the two-mass system and the torque required to accelerate the rigid body is called correction couple and this couple must be applied, when the masses are placed arbitrarily to make the system dynamical equivalent.
2. The sum of torques required to accelerate a 2 mass system and to accelerate a rigid body is called correction couple.
a) True
b) False
View Answer
Explanation: Difference between the torques required to accelerate the two-mass system and the torque required to accelerate the rigid body is called correction couple.
3. The correction couple does not depend on _________
a) Distance between arbitrary masses
b) Distance between the two masses for a true dynamically equivalent system
c) Radius of gyration of equivalent system
d) Distance between fixed masses
View Answer
Explanation: Distance between arbitrary masses, Distance between the two masses for a true dynamically equivalent system and Radius of gyration of equivalent system all effect the correction couple.
4. In the figure given below, A and D are arbitrary masses placed Quantity L is known as _______
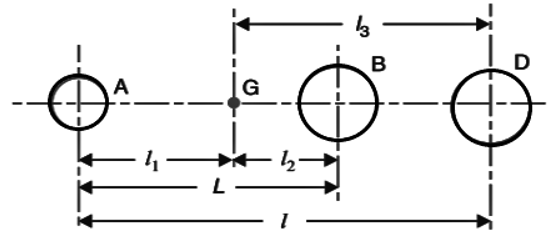
a) Distance between the two masses for a true dynamically equivalent system
b) Distance between fixed masses
c) Distance between arbitrary masses
d) Equivalent radius
View Answer
Explanation: The distance between the two masses for a true dynamically equivalent system is given by L and has the expression of (Kg2 + l12)/l1.
5. An Internal combustion engine has a connecting rod of mass 2 kg and the distance between the centre of crank and centre of gudgeon pin is 25 cm. The Center of Gravity lies at a point 10 cm from the gudgeon pin along the line of centres. The radius of gyration of this system about an axis through the Center of Gravity perpendicular to the plane of rotation is 11 cm. Find the mass located at gudgeon pin in Kg.
a) 0.9
b) 0.8
c) 1.1
d) 1.2
View Answer
Explanation: From the given data l = 25 cm, l1 = 10cm kg=11cm
l1.l2=kg2, l2 = 12.1 cm
M= l2m/( l1+ l2)
= 12.1x 2/( 12.1 + 10)
= 1.1 Kg.
6. From the data given:
54tr xc
Connecting rod of mass 2 kg and the distance between the centre of crank and centre of gudgeon pin is 25 cm. The Center of Gravity lies at a point 10 cm from the gudgeon pin along the line of centres.
The radius of gyration of this system about an axis through the Center of Gravity perpendicular to the plane of rotation is 11 cm.
Find the mass placed at distance l2 from center of gravity.
a) 0.9
b) 0.8
c) 1.1
d) 1.2
View Answer
Explanation: From the given data l = 25 cm, l1 = 10cm kg=11cm
l1.l2=kg2, l2 = 12.1 cm
M = l1.m/( l1+ l2)
= 10×2(10+12.1)
= 0.9 kg.
7. An Internal combustion engine has a connecting rod of mass 2 kg and the distance between the centre of crank and centre of gudgeon pin is 25 cm. The Center of Gravity lies at a point 10 cm from the gudgeon pin along the line of centres. The radius of gyration of this system about an axis through the Center of Gravity perpendicular to the plane of rotation is 11 cm. If two masses are used instead of the connecting rod, one at the gudgeon pin and other at the crank pin. What will be the new radius of gyration?
a) 0.212m
b) 0.122m
c) 0.1m
d) 0.145m
View Answer
Explanation: Let l3 be the distance between the masses, then l3 = l- l1 = 15cm
If K1 is the new radius of gyration then, K12= l1. l3 = 0.1×0.15 = 0.015 m2
Therefore, K1 = 0.122 m.
8. Mass moment of inertia of two arbitrary masses placed will be same as the mass moment inertia of the rigid body.
a) True
b) False
View Answer
Explanation: Mass moment of inertia of two arbitrary masses placed will be different as the mass moment inertia of the rigid body, this is why there is a need to calculate the correction couple.
9. An Internal combustion engine has a connecting rod of mass 2 kg and the distance between the centre of crank and centre of gudgeon pin is 25 cm. The Center of Gravity lies at a point 10 cm from the gudgeon pin along the line of centres. The radius of gyration of this system about an axis through the Center of Gravity perpendicular to the plane of rotation is 11 cm. If two masses are used instead of the connecting rod, one at the gudgeon pin and other at the crank pin, if the angular acceleration of the rod is 23 000 rad/s2, then find the correction couple in N-m.
a) 140.2
b) 133.4
c) 136.8
d) 135.6
View Answer
Explanation: We know that correction couple is given by T’ = m.(k12 – kg2).α
T’ = 2. (0.015 – 0.112). 23000
= 133.4 N-m.
Sanfoundry Global Education & Learning Series – Machine Dynamics.
To practice all questions papers on Machine Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Practice Aeronautical Engineering MCQs
- Check Dynamics of Machinery Books
- Practice Mechanical Engineering MCQs
- Apply for Aerospace Engineering Internship
- Apply for Mechanical Engineering Internship
