This set of Tough Machine Dynamics Questions and Answers focuses on “Balancing of a Single Rotating Mass By Two Masses Rotating in Different Planes”.
1. Let the disturbing mass be 50 Kg, with radius of rotation = 0.1m, if one of the balancing mass is 30 Kg at a radius of rotation 0.1m then find the other balancing mass situated at a distance of 0.2m.
a) 80
b) 40
c) 20
d) 10
View Answer
Explanation: mr = m1mr + m2r2
50×0.1 = 30×0.1 + m2x0.2
5=3 + 0.2m
m2=10 Kg.
2. A single mass defect needs to be balanced by a single balancing mass
a) True
b) False
View Answer
Explanation: A single mass defect lying on a single plane can be countered with the help of different masses lying on different planes with the defective mass either being at center or to the either side.
3. In a system two masses are used to balance the unbalanced forces. Find the mass of the balancing mass which has to be situated at a distance of 20cm, if the disturbing mass is of 100 Kg having radius of rotation of 0.1m. One of the balancing mass is 30 Kg with RoR of 10cm.
a) 70
b) 35
c) 20
d) 10
View Answer
Explanation: For a balanced system
m.r = m1r + m2r2
100×0.1 = 30×0.1 + m2x0.2
10=3 + 0.2m
m2=35 Kg.
4. In the given figure, m1=20 Kg, m2=30Kg and m=50 Kg, if r1=0.2m and r=0.3m, l=1m, find l2.
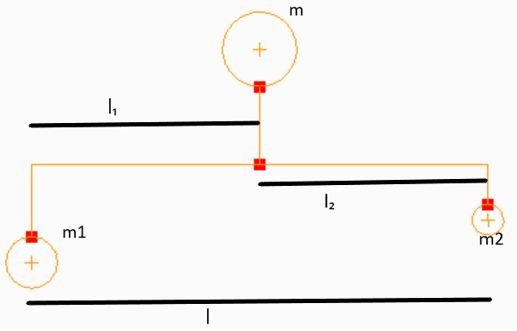
a) 0.26m
b) 0.52m
c) 1.04m
d)0.13m
View Answer
Explanation: M1r1l = mrl2
20×0.2×1 = 50 x 0.3 xl2
4 = 15xl2
l2 = 0.26m.
5. In the given figure, m1=10, Kg m2=30Kg and m=50 Kg, if r1=0.2m and r=0.3m, l=1m, find l2.

a) 0.26m
b) 0.52m
c) 1.04m
d) 0.13m
View Answer
Explanation: M1r1l = mrl2
10×0.2×1 = 50 x 0.3 xl2
2 = 15xl2
l2 = 0.13m.
6. In the given figure, m1=10 Kg, m2=30Kg and m=50 Kg, if r=0.3m, l=1m, find l2 = 0.5m, find r1 in m.

a) 1.5
b) 0.75
c) 3
d) 6
View Answer
Explanation: M1r1l = mrl2
10xr1x1 = 50 x 0.3 x0.5
10r1 = 7.5
l2 = 0.75m.
7. Unbalanced mass leads to vibrations.
a) True
b) False
View Answer
Explanation: The unbalanced forces not only increase the loads on bearings and stresses in the various members, but also produce unpleasant and even dangerous vibrations.
8. Which of the following statement is correct?
a) In any engine, 100% of the reciprocating masses can be balanced dynamically
b) In the case of balancing of multicylinder engine, the value of secondary force is higher than the value of the primary force
c) In the case of balancing of multimass rotating systems, dynamic balancing can be directly started without static balancing done to the system
d) none of the mentioned
View Answer
Explanation: None.
Sanfoundry Global Education & Learning Series – Machine Dynamics.
To practice tough questions and answers on all areas of Machine Dynamics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
- Apply for Mechanical Engineering Internship
- Check Mechanical Engineering Books
- Check Aeronautical Engineering Books
- Apply for Aerospace Engineering Internship
- Check Dynamics of Machinery Books
