This set of Engineering Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Moment of a Force on a Specified Axis”.
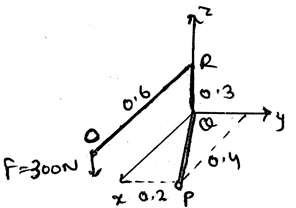
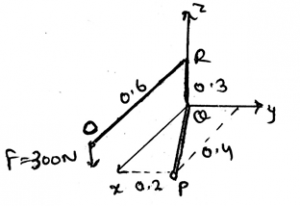
1. Determine the moment’s magnitude produced by the force as shown in the diagram, which tends to rotate the rod ORQP along QP.
a) 80.49 Nm
b) 72.12 Nm
c) -36.67 Nm
d) 36.67 Nm
View Answer
Explanation: The use of the formula A.(rxF) gives the answer. In which A is 0.89i + 0.447j m. And the force is 300N, which is being applied at the end of the rod. Thus, after finding the equation of the axis and then replacing it in the equation shown above we get the answer. Actually, the main task is to know the axis equation in the vector form. Then get the magnitude of the moment.
2. The calculation of the moment about the axis and the moment about any point by a force applied on the body are different from each other.
a) True
b) False
View Answer
Explanation: The calculation of the moment about the axis and the moment about any point by a force applied on the body are different from each other. It is because both of the calculations require different formulas. And both of the formulas have different inputs, which is obviously different.
3. In the calculation of the moment of the force about the axis, the cross product table, i.e. the 3X3 matrix which is made for doing the cross product having 3 rows, contains three elements. Which are they from top to bottom?
a) Axis coordinates, point coordinates, and the force coordinates
b) Point coordinates, axis coordinates, and the force coordinates
c) Axis coordinates, force coordinates, and the point coordinates
d) Force coordinates, point coordinates, and the axis coordinates
View Answer
Explanation: The 3X3 matrix which is being made is having axis coordinates, point coordinates and the force coordinates. They are from top to bottom placed. The order cannot be changed. Or if changed then one needs to apply the negative sign appropriately. Negative because the directions get reversed.
4. Which of the following is correct? (For A representing the vector representation of the axis of rotation, r the radius vector and F the force vector)
a) A.(rxF)
b) Ax(rxF)
c) A.(r.F)
d) Fx(r.F)
View Answer
Explanation: The correct form of the equation is given by A.(rxF). Where A represents the vector representation of the axis of rotation, r the radius vector and F the force vector. This is usually done for determining the moment of the force about the axis. That is if the body is being rotated by the force about an axis.
5. In the equation A.(rxF), the r vector is what?
a) The magnitude of the axis, i.e. the length of the axis
b) The length of the force vector
c) The length of the radius
d) The radius vector
View Answer
Explanation: The r in the equation A.(rxF) is the radius vector. That is it is the vector which is having the start point at the axis and the endpoint at the point of action of the force on the body. This vector is being crossed by the force vector, which is then followed by the dot product with the axis vector.
6. The axis vector in the calculation of the moment along the axis of rotation is the axis which is collinear with the force vector.
a) True
b) False
View Answer
Explanation: The axis of the rotation cannot be collinear with the force vector. If it does so then the rotation of body is not possible. That is the moment of the force is zero. Which means no rotation is given by the force along the axis of rotation of the body.
7. Which of the following is correct?
a) We cannot represent the moment caused by the force along any axis in vector form
b) We can represent the moment caused by the force along any axis in the scalar form
c) We cannot represent the moment caused by the force along any point in vector form
d) We can represent the moment caused by the force along any axis in vector form
View Answer
Explanation: As moment is a vector, we can represent it in the vector form easily. Whether it may be the moment of the force acting on the body about the axis, or about the point. We can also convert the same in the Cartesian form too. The only thing we need to do is the cross product of the radius vector and the force vector.
8. What if the perpendicular distance from the axis is infinity?
a) The rotation is not possible
b) The rotation is possible but the moment generated is very less
c) The force applied will be very much high for even a small rotation
d) No rotation unless the contact is being broken
View Answer
Explanation: The long distance means a huge force which one needs to apply. Because distance increased will also increase the resistance inertia which will obviously increase the force required for the rotation. Though we know that the larger the distance the small is the force applied for rotation. But inertia must be taken into the considerations sometimes.
9. In the equation A.(rxF) the r is heading from ______________ and ending at _____________
a) Axis of rotation, Force vector
b) Axis of rotation, Force vector’s point of action on the body
c) Force vector, Axis of rotation
d) Force vector’s point of action on the body, Axis of rotation
View Answer
Explanation: It is the radius vector. The radius vector is always from the axis of rotation to the point of action of the force on the body. Which means that the radius vector is not on any point on the force vector. Rather it ending at the point on the force vector, where it is being in contact of the body.
10. What if the moment of the force calculated about the axis is negative?
a) It means that the force is applied in the opposite direction as imagined
b) It means that the direction of the motion is in the opposite sense as imagined
c) It means that the radius vector is in the opposite sense as imagined
d) Such calculation means that the calculations are wrongly done
View Answer
Explanation: It means that the direction of the motion is in the opposite sense as imagined. We can’t say about the direction of the force or the direction of the radius vector. But yes we can say about the direction of the rotation as it the thing which is going to be calculated. Rest all the parts are fixed. They can’t be altered.
11. Determine the moment MQP in the vector form produced by the force as shown in the diagram, which tends to rotate the rod ORQP along QP.
a) 72i + 36j Nm
b) 72i – 36j Nm
c) -72i – 36j Nm
d) -72i + 36j Nm
View Answer
Explanation: The use of the formula A.(rxF) gives the answer. In which A is 0.89i + 0.447j m. And the force is 300N, which is being applied at the end of the rod. Thus, after finding the equation of the axis and then replacing it in the equation shown above we get the answer. Actually, the main task is to know the axis equation in the vector form.
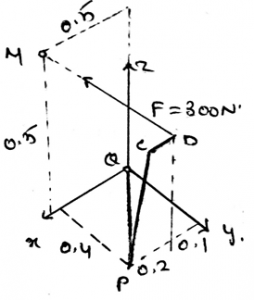
12. Determine the moment of the force F along the segment QP of the pipe assembly shown in the figure.
a) 110Nm
b) 100Nm
c) 500Nm
d) 510Nm
View Answer
Explanation: The use of the formula A.(rxF) gives the answer. In which A is 0.6i + 0.8j m and the r is 0.5i + 0.5k. And the force is 300N, which is being applied at the end of the rod. Thus, after finding the equation of the axis and then replacing it in the equation shown above we get the answer. Actually, the main task is to know the axis equation in the vector form. Then get the magnitude of the moment.
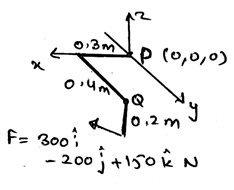
13. Determine the magnitude of the moment of the force about the axis PQ.
a) -72Nm
b) 82Nm
c) 90Nm
d) 50Nm
View Answer
Explanation: The use of the formula A.(rxF) gives the answer. In which A is 0.6i + 0.8j m and the r is -0.2k, and the force which is being applied at the end of the rod. Thus, after finding the equation of the axis and then replacing it in the equation shown above we get the answer. Actually, the main task is to know the axis equation in the vector form. Then get the magnitude of the moment.
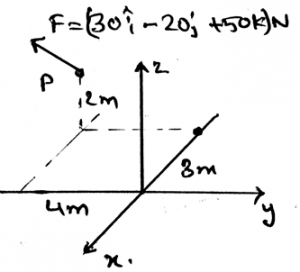
14. Determine the magnitude of the moment of the force about the y-axis.
a) -72Nm
b) 82Nm
c) 210Nm
d) 50Nm
View Answer
Explanation: The use of the formula A.(rxF) gives the answer. In which A is 1j m and the r is -3i + 4j + 2k and the force which is being applied at the end of the rod. Thus, after finding the equation of the axis and then replacing it in the equation shown above we get the answer. Actually, the main task is to know the axis equation in the vector form. Then get the magnitude of the moment.
15. The ___________ forces do not cause the rotation if the rotation is considered in about the axis of the body or the centroid axis of the body.
a) Non-concurrent
b) Concurrent
c) Parallel
d) Non-Parallel
View Answer
Explanation: The concurrent forces are the which are somewhere touching the axis of rotation. If any of the force is touching that axis, that force is not considered or is insufficient to cause a rotation. If a force is concurrent then the perpendicular distance of the force from the line of an axis is zero, thus no rotation. As we know rotation is caused by a moment.
Sanfoundry Global Education & Learning Series – Engineering Mechanics.
To practice all areas of Engineering Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]