This set of Engineering Mechanics Questions and Answers for Freshers focuses on “Cartesian Vectors – 2”.
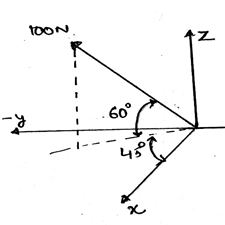
1. Express the vector in the Cartesian Form, if the angle made by it with y and z axis is 60˚ and 45˚ respectively. Also, it makes an angle of α with the x-axis. The magnitude of the force is 200N.
a) 100i + 100j + 141.4k N
b) 100i – 100j + 141.4k N
c) 100i + 100j – 141.4k N
d) 100i – 100j – 141.4k N
View Answer
Explanation: When you will resolve the vector in its x, y and z-axis components, you will get an equation containing cosα. After getting the correctly, you need to directly put that value in the previous equation of components.
2. In the figure given below, with F1 = 60j + 80k and F2= 50i -100j + 100k, what is the value of β? (β is the angle made by the resultant vector with the y-axis )
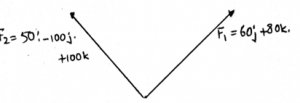
a) 76˚
b) 102˚
c) 19˚
d) 130˚
View Answer
Explanation: Just add the two vectors in their Cartesian form only. After that you will get the resultant vector in the Cartesian form. After that just divide the y-axis component’s magnitude by the resultant of the vector. You will get cosβ.
3. In the figure given below, calculate the value of cosγ. (γ is the angle made by the resultant vector and the z-axis)
a) 0.866
b) -0.354
c) 0.540
d) 0.354
View Answer
Explanation: Well, the question is just a tricky one. Just subtract 60 from 90, you will get the γ, which is 30. And then apply the cosine formula for getting the components of the respective axis.
4. What is the magnitude of the vector, 12i – 8j – 24k?
a) 18
b) 28
c) 38
d) 48
View Answer
Explanation: 122 + 82 + 242 = 282 . After you get this, the 28 is the magnitude. This is the using of distance formula between two Cartesian points. Considering the point (12, -8, -24) and then calculating the distance from the origin.
5. The coordinate of the Force vector AB is A (2, 0, 2) and B (-2, 3.46, 3). What are its directions?
a) -0.742i + 0.643j + 0.186k
b) 0.742i – 0.643j – 0.186k
c) -0.742i – 0.643j + 0.186k
d) -0.742i + 0.643j – 0.186k
View Answer
Explanation: First subtract the coordinates of the A form B. And place the x, y and z-axis coordinate separated by i, j and k respectively. Like Ai + Bj + Ck , if A, B and C are the x, y and z-axis coordinates. You will get a Cartesian vector, just find its magnitude and divide it with the vector.
6. The coordinate of the Force vector AB is A (2, 0, 2) and B (-2, 3.46, 3). It has a magnitude of 750N. Which is the best Cartesian representation of the vector AB?
a) -557i + 482j + 139k N
b) -557i – 482j + 139k N
c) -557i + 482j – 139k N
d) 557i – 482j – 139k N
View Answer
Explanation: First try to make the unit vector of AB. Then you will get the Cartesian form of unit vector, after that just multiply 750 scalar quantity with it. Which means you are first taking out the desired direction and then multiplying the scalar to get the desired vector in the desired direction.
7. A force vector is along 4i – 4k direction and has a magnitude 100N and another force vector is along 4i +2j -4k and has a magnitude of 120N. What is the resultant of both forces?
a) 80i + 40j – 80k N
b) 80i – 40j – 80k N
c) 151i + 40j – 80k N
d) 151i+ 40j – 151k N
View Answer
Explanation: Just make the unit vectors of the given directions of the vectors and then multiply them with their respective magnitudes, after than you will get two vectors in the Cartesian form. Just add them.
8. The value cos-1(-3/7) + cos-1(2/7) + cos-1(6/7) is ____________
a) 215.4˚
b) 273.4˚
c) 188.4˚
d) 219.4˚
View Answer
Explanation: It’s a calculative question, but still can be solved if you construct the triangle of the respective cosine inverses given, then convert them in the tangent form then use log table, if necessary. Or the use of a calculator is also good if permissible. Or you can make use of triangle laws to obtain the same.
9. Two vectors emerging from a point are always in a single plane.
a) True
b) False
View Answer
Explanation: Yes, whenever two vectors are there, they are always in a single plane. If the emerging vectors are more than three then saying about their plane is somewhat difficult. But for two vectors it seems easy to understand about their plane.
10. Three vectors emerging from a point are always in a single plane.
a) True
b) False
View Answer
Explanation: Yes, whenever two vectors are there, they are always in a single plane. But you cannot say about the three vectors, they may or may be. Because if the emerging vectors are more than three then saying about their plane is somewhat difficult. But for two vectors it seems easy to understand about their plane.
11. What is the magnitude of the unit vector?
a) √3
b) √2
c) 1
d) 0
View Answer
Explanation: The magnitude of the unit vector is always = 1. This means unit vector is the vector in the direction of the original vector and the magnitude of the same is unity. And unit vector is always in the direction of its vector.
12. What is the difference between a position vector and unit vector?
a) Position vector has magnitude = 1 and direction, while the unit vector has magnitude = 0 and no direction
b) Position vector has magnitude = 0 and direction, while unit vector has magnitude = 0 and no direction
c) Position vector has some magnitude and direction, while the unit vector has magnitude = 0 and no direction
d) Position vector has some magnitude and direction, while the unit vector has magnitude = 1 and a specified direction
View Answer
Explanation: As position vector defines the position of the point in the Cartesian plane with respect of the origin, it will definitely have a direction and also a magnitude. Unit vector is a vector whose magnitude is = 1 and is having a specific direction.
13. What if we multiply a scalar to the unit vector?
a) The direction will change accordingly
b) The magnitude will change accordingly
c) The magnitude will not change accordingly
d) The direction will change by a factor of square root of the scalar
View Answer
Explanation: The magnitude of the unit vector will change by the amount of the scalar multiplied. Not the direction. Because the direction is being fixed after the application of the unit vector’s calculation. That is the vector divided by its magnitude.
14. Which is true for the vector provided the only position coordinates given?
a) (Final position coordinates + initial positions coordinates) gives the vector form of the vector
b) (Final position coordinates – initial positions coordinates) gives the vector form of the vector
c) (Initial positions coordinates – Final position coordinates) gives the vector form of the vector
d) (Initial positions coordinates + Final position coordinates) gives the vector form of the vector
View Answer
Explanation: We find the vector form from subtracting the initial position coordinates from final position coordinates. Not from subtracting the final position coordinates from initial position coordinates.
15. A vector can always have_____________
a) Only one component along any of the axis
b) Only two components along any of the axis
c) Only three components along any of the axis
d) A unit vector along the direction perpendicular to its direction
View Answer
Explanation: All vectors have three components, whether they are zero or not. And unit vector is always in the direction of its vector. And the unit vector has the magnitude equal to unity. This means unit vector is the vector in the direction of the original vector and the magnitude of the same is unity.
Sanfoundry Global Education & Learning Series – Engineering Mechanics.
To practice all areas of Engineering Mechanics for Freshers, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]