This set of Engineering Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Cartesian Vectors – 1”.
1. In right handed coordinate system which axis is considered to be positive?
a) The thumb is z-axis, fingers curled from x-axis to y-axis
b) The thumb is x-axis, fingers curled from z-axis to y-axis
c) The thumb is y-axis, fingers curled from x-axis to z-axis
d) The thumb is z-axis, fingers curled from y-axis to x-axis
View Answer
Explanation: As right handed coordinate system means that you are curling your fingers from positive x-axis towards y-axis and the thumb which is projected is pointed to the positive z-axis. Thus visualizing the same and knowing the basic members of the axis will not create many problems.
2. If A is any vector with Ai + Bj + Ck then what is the y-axis component of the vector?
a) B units
b) A units
c) C units
d) Square root of a sum of squares of the three, i.e. A, B and C
View Answer
Explanation: As the given vector is shown in the Cartesian system, the number with “j” is the Y-axis component of the given vector. With the numbers with “i” representing components of x-axis and “k” representing the z axis respectively.
3. If the force vector F is having its x-axis component being equal to Z N, y-axis component be X N and z-axis component be Y N then vector F is best represented by?
a) Xi + Yj + Zk
b) Yi + Xj + Zk
c) Zi + Yj + Xk
d) Zi + Xj + Yk
View Answer
Explanation: It is given that x, y and z-axis components are Z, X and Y respectively. Thus, just by placing the right coordinates we get option d to be correct. Here just the interchange of the axis’s representor with their respective axis is creating confusion. Which must be figured out.
4. Which statement is right for force vector F = Ai + Bj + Ck?
a) In rectangular components representation of any vector we have vector F = Ai + Bj + Ck
b) In rectangular components representation of any vector we have vector F = Ax + By + Cz
c) In rectangular components representation of any vector we have vector F = Fx + Fy + Fz
d) In rectangular components representation of any vector we have vector F = Fi + Fj + Fk
View Answer
Explanation: As given the vector is F = Ai + Bj + Ck, this implies that the x ,y and z-axis components of this vector is A, B and C respectively. But, in rectangular components representation of any vector, the vector is written as F = Fx + Fy + Fz.
5. What is the magnitude of the Cartesian vector having the x, y and z axis components to be A, B and C?
a) Square root of the squares each A, B and C
b) Square of the squares each A, B and C
c) Cube root of the squares each A, B and C
d) Cube of the squares each A, B and C
View Answer
Explanation: The magnitude of a Cartesian vector having the x, y and z axis components to be A, B and C is always the square root of the squares each A, B and C. This comes from the distance formula between two points in the Cartesian plane. That is the square root of the subtraction of the final and initial point of a line.
6. What is cosα for force vector F = Ax + By +Cz (Given α, β and γ are the angles made by the vector with x, y and z axis respectively)?
a) B/F
b) C/F
c) A/F
d) 1
View Answer
Explanation: The cosine component of the vector is defined as the ratio of the x-axis component to the magnitude of the vector, i.e. F in this case. Likewise, the sine component is the ratio of the y-axis component to the magnitude of the vector.
7. What is the sum of squares of the cosine angles made by the force vector with the coordinate axis?
a) 1
b) ½
c) 2
d) 3
View Answer
Explanation: The sum of the squares of the cosines of the vector will give you the squares of the components in the numerator, and the vector’s magnitude’s square in the denominator. But the numerator sum is equal to the vector’s magnitude’s square. Thus, the answer = 1.
8. What is the x-axis component of the force vector Ai + Bj +Ck with magnitude equal to F?
a) B
b) C
c) Fcosα
d) Fcosβ
View Answer
Explanation: As we know that the cosα is the ratio of the x-axis component to the magnitude of the vector. Thus the x-axis components is Fcosα, F, the magnitude in the case. Likely if we want to take the y-axis component we would try to do the same with the sine component.
9. We can add the force vectors directly. But with dividing each by it’s magnitude first.
a) True
b) False
View Answer
Explanation: False, because if you will divide the magnitude of the vector to itself than the resulting would be the unit vector. Which is just giving you the direction of the vector, not the vector itself. This means unit vector has direction same as it’s respective vector but having a magnitude equal to one.
10. For a vector F, Fcosβ is equal to zero. What does this refer?
a) X-axis component is zero
b) Y-axis component is zero
c) Z-axis component is zero
d) β = 180˚
View Answer
Explanation: As we know the α, β and γ are the angles made by the x, y and z-axis respectively. Thus y-axis component is zero, or β = 90˚. And thus if the angle is giving component to be zero this means the vector in that particular axis is perpendicular to that axis.
11. Which statement is correct about the vector F?
a) F= Fcos β + Fcos α + Fcosγ
b) F= Fsin β + Fcos α + Fcosγ
c) F= Fcos β + Fsin α + Fcosγ
d) F= Fcos β + Fcos α + Fsinγ
View Answer
Explanation: As we know the α, β and γ are the angles made by the x, y and z-axis respectively. Thus, is the magnitude of the vector is F, the F= Fcos β + Fcos α + Fcosγ. Which means the force is the resultant of all its axis’ components.
12. Which is true?
a) ∑F = ∑Fx + ∑Fy + ∑Fz
b) ∑F = -(∑Fx + ∑Fy + ∑Fz)
c) ∑F = ∑Fxi + ∑Fyj + ∑Fzk
d) ∑F = -(∑Fxi+ ∑Fyj + ∑Fzk)
View Answer
Explanation: The total of two or more forces is equal to the sum of their respective axis’s components. That is the resultant adds up all the components of the forces in their respective axis, whether it may be x, y or z axis.
13. Find the angle α, for the vector making an angle by y and z axis as 60˚ and 45˚ respectively. It makes an angle of α with x-axis. The magnitude of the force is 200N.
a) 60˚
b) 120˚
c) 45˚
d) 90˚
View Answer
Explanation: When you will resolve the vector in its x, y and z-axis components, you will get an equation containing cosα. After getting the α correctly, you need to directly put that value in the previous equation of components. α = 60˚. As 120˚ will give a negative component. Just try to resolve the vector in its components.
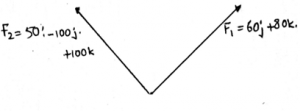
14. What is the magnitude of the resultant force when F1 = 60j + 80k and F2 = 50i – 100j + 100k?
a) 188 unit
b) 191 unit
c) 181 unit
d) 120 unit
View Answer
Explanation: Just do the vector addition. And then calculate the resultant of the sum you get. In vector addition just use the x, y and z axis components and then add them separately which will give you the resultant’s components. Now do the pythogerous method of square rooting of components and the resultant is what you get.
15. Express F = 100 N (shown in the figure below) as a Cartesian vector.
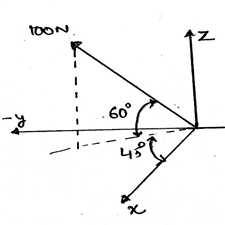
a) 35.4i – 35.4j + 86.6k
b) 35.4i – 35.4j – 86.6k
c) 35.4i – 35.4j – 86.6k
d) 35.4i + 35.4j + 86.6k
View Answer
Explanation: Try to resolve the given vector so that you will get respective components. Use sine and cosine multiplication of the angles given to calculate the components. Also, try to use the angles given in the diagram which will be an easier way to solve the question and getting the answer.
Sanfoundry Global Education & Learning Series – Engineering Mechanics.
To practice all areas of Engineering Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]