This set of Engineering Mechanics Questions and Answers for Aptitude test focuses on “Moments of Inertia for an Area About Inclined Axis – 2”.
1. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) u = xcosθ + ysinθ
b) u = xcosθ – ysinθ
c) u = ycosθ + xsinθ
d) u = ycosθ – xsinθ
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
2. In the calculations of moments of inertia for an area about inclined axis we use the product of a moment of inertia. It is the the sum of _____________ and _________________
a) Area and volume
b) Volume and linear distance
c) Moment of inertia at centroid and the product of the area and del dx and del dy
d) Moment of inertia at base and the product of the area and del dx and del dy
View Answer
Explanation: The product of moment of inertia is required as to design the structure of the body. This means that the designing of the body is majorly done by the help of the determination of the product of the moment of Inertia.
3. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) Iu = Ix cos2θ + Iysin2θ – 2Ixycosθsinθ
b) Iv = Ixcos2θ + Iysin2θ – 2Ixycosθsinθ
c) Iu = Ixcos2θ + Iysin2θ – 2Ixycosθsinθ
d) Iv = Ixcos2θ + Iysin2θ + 2Ixycosθsinθ
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
4. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
5. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) v = xcosθ + ysinθ
b) v = xcosθ – ysinθ
c) v = ycosθ + xsinθ
d) v = ycosθ – xsinθ
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
6. There is parallel axis theorem for the area, and it is can be used to determine the moment of inertia of an area about inclined axis.
a) True
b) False
View Answer
Explanation: There is no perpendicular axis theorem for the area. In spite, there is the theorem as parallel axis for any area. Thus we have the theorem which is used to add the two mutually perpendicular moment of inertias.
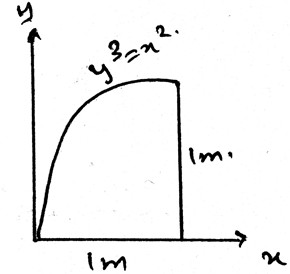
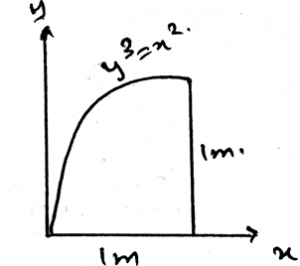
7. Determine the moment of inertia of the area about the y-axis.
a) 0.273m2
b) 11m2
c) 0.141m2
d) 0.811m2
View Answer
Explanation: Parallel axis for any area is used to add the two mutually perpendicular moment of inertias for areas. It gives a moment of inertia perpendicular to the surface of the body. That is the moment of inertia perpendicular to the surface in considerance.
8. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
9. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) Iu = Ixcos2θ + Iysin2θ – 2Ixycosθsinθ
b) Iv = Ixcos2θ + Iysin2θ – 2Ixycosθsinθ
c) Iu = Ixcos2θ + Iysin2θ – 2Ixycosθsinθ
d) Iv = Ixcos2θ – Iysin2θ + 2Ixycosθsinθ
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
10. Moment of Inertia about an inclined axis is the integration of the cube of the distance of the centroid and the del area along the whole area of the structure and after this calculations, we multiply the moment of areas.
a) True
b) False
View Answer
Explanation: The moment of inertia of the section is the integration of the square of the distance of the centroid and the del area along the whole area of the structure. This is having much significance in the various fields in the engineering sector. The main types are the ‘I’ section structures which are being much used.
11. Determine the moment of inertia of the area about the x-axis.
a) 0.111m2
b) 11m2
c) 0.141m2
d) 0.811m2
View Answer
Explanation: None.
12. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
13. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
14. In the calculations of the moment of inertia of the area about an inclined axis, we have some transformation done. They are:
a) Iuv = Ixcosθsinθ – Iysinθcosθ + Ixy (cos2θ-sin2θ)
b) Iuv = Ixcosθsinθ + Iysinθcosθ – Ixy (cos2θ-sin2θ)
c) Iuv = Ixcosθsinθ – Iysinθcosθ – Ixy (cos2θ-sin2θ)
d) Iuv = Ixcosθsinθ + Iysinθcosθ + Ixy(cos2θ-sin2θ)
View Answer
Explanation: In the moment of inertia calculations we see that the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading. Thus when there is the inclination of the axis, we use transformation.
15. If any external moment along with the force is applied on the structure and we are determining the moment of inertia for areas about inclined axis then what should we consider?
a) The net force will act at the centroid of the structure only
b) The net load will not be formed as all the forces will be cancelled
c) The net force will act on the base of the loading horizontally
d) The net force will not be considered, there would be a net force of the distribution, rest will be the external forces
View Answer
Explanation: The external forces are treated differently. They are not added by the force of the distributed loading. That is the force not only acts at the centroid always. It can be shifted also. Depending on the external forces. Thus the use of centroid or centre of mass.
Sanfoundry Global Education & Learning Series – Engineering Mechanics.
To practice all areas of Engineering Mechanics for Aptitude test, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]