This set of Engineering Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Theorem of Pappus and Guldinus”.
1. The theorem of Pappus and Guldinus is used to find the ____________
a) Surface area of the body
b) Surface area of the body of revolution
c) Surface area of the body of linear motion
d) Surface area of the body of rectangular motion
View Answer
Explanation: The theorem is used to find the surface area and the volume of the revolving body. This is done by using simple integration. Thus the surface area and the volume of any 2D curve being rotated can be made to be calculated from this theorem.
2. The theorem of Pappus and Guldinus states that the area of the revolving curve is ______________
a) Product of the area, length of the generated curve and the radius vector
b) Product of the area, length of the generated curve and the perpendicular distance from axis
c) Product of the volume, length of the generated curve and the radius vector
d) Product of the volume, length of the generated curve and the perpendicular distance from axis
View Answer
Explanation: The theorem is used to find the surface area and the volume of the revolving body. This is done by using simple integration. Thus the surface area and the volume of any 2D curve. It is just the product of the area, length of generated curve and the perpendicular distance from axis.
3. Product of the area, ______________________ and the perpendicular distance from axis are being used in the theorem to find the area of the revolution.
a) Length of generated curve
b) Length of generated radius
c) Length of generated length vector
d) Length of generated area vector
View Answer
Explanation: The theorem is used to find the surface area and the volume of the revolving body. This is done by using simple integration. Thus the surface area and the volume of any 2D curve. It is just the product of the area, length of the generated curve and the perpendicular distance from the axis.
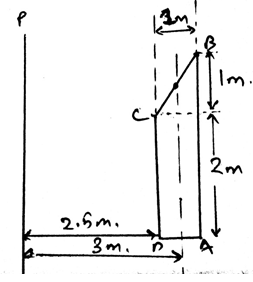
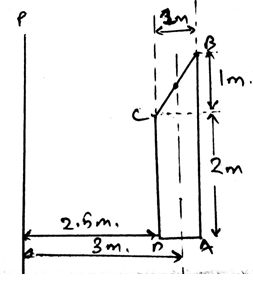
4. Determine the surface area of the structure when rotated about the ray P.
a) 134m2
b) 143m2
c) 154m2
d) 169m2
View Answer
Explanation: The theorem is used to find the surface area and the volume of the revolving body. This is done by using simple integration. Thus the surface area and the volume of any 2D curve. It is just the product of the area, length of the generated curve and the perpendicular distance from the axis.
5. The distance used in the theorem is the distance travelled by ______________
a) Body
b) Body’s centroid
c) Body’s length vector
d) Body’s radius vector
View Answer
Explanation: The theorem is used to find the surface area and the volume of the revolving body. Thus the surface area and the volume of any 2D curve. It is just the product of the area, length of generated curve and the perpendicular distance from axis. The distance being the distance travelled by the centroid.
6. Product of the Volume, ______________________ and the perpendicular distance from axis are being used in the theorem to find the volume of the revolution.
a) Area of generated curve
b) Area of generated radius
c) Area of generated length vector
d) Area of generated area vector
View Answer
Explanation: The theorem is used to find the surface area and the volume of the revolving body. This is done by using simple integration. Thus the surface area and the volume of any 2D curve. It is just the product of the volume, area of generated curve and the perpendicular distance from axis.
7. The maximum value of the frictional force that can be applied to the composite body under which the theorem of the Pappus and Guldinus is going to be applied is called _________
a) Limiting Friction
b) Non-Limiting Friction
c) Limiting Action Friction
d) Non-Limiting Action Friction
View Answer
Explanation: The friction is the phenomena that define that there is a resistance which is present there between the two surfaces. The two surfaces are in contact and the friction applies at that surface only, resisting the motion of the surface. Thus the maximum values is called as limiting friction.
8. When the body which is applied forces come in the stage of the limiting friction then the body over which this theorem is to be applied is termed as to come in ___________ equilibrium.
a) Unstable
b) Stable
c) Non-stable
d) Improper Stable
View Answer
Explanation: As the limiting friction is the maximum value of the frictional forces. Thus if more force is applied to the body then the body is going to move forward. Because the two surfaces are in contact and the friction applies at that surface only, resisting the motion of the surface. Thus the name unstable equilibrium.
9. Determine the volume of the structure when rotated about the ray P.
a) 47.6m3
b) 43m3
c) 14m3
d) 19m3
View Answer
Explanation: None.
10. We use sometimes the measures to know the direction of moment. It is done by right handed coordinate system. Which is right about it for the bodies over which this theorem is going to be applied (consider the mentioned axis to be positive)?
a) Thumb is z-axis, fingers curled from x-axis to y-axis
b) Thumb is x-axis, fingers curled from z-axis to y-axis
c) Thumb is y-axis, fingers curled from x-axis to z-axis
d) Thumb is z-axis, fingers curled from y-axis to x-axis
View Answer
Explanation: As right handed coordinate system means that you are curling your fingers from positive x-axis towards y-axis and the thumb which is projected is pointed to the positive z-axis. Thus visualizing the same and knowing the basic members of axis will not create much problem.
11. What is not the condition for the equilibrium in three dimensional system of axis for the bodies for which this theorem is going to be applied?
a) ∑Fx=0
b) ∑Fy=0
c) ∑Fz=0
d) ∑F≠0
View Answer
Explanation: For the equilibrium in the three dimensional system of axis we have all the conditions true as, ∑Fx=0, ∑Fy=0 and ∑Fz=0. Also, we have the summation of the forces equal to zero. Which is not a non-zero value.
12. What is a collinear system of forces for the bodies over which this theorem is to apply?
a) The force system having all the forces parallel to each other
b) The force system having all the forces perpendicular to each other
c) The force system having all the forces emerging from a single point
d) Forces cannot form a collinear system of forces, it is not possible
View Answer
Explanation: The force system having all the forces emerging from a point is called the collinear system of force. This is a type of system of the force, which is easy in the simplification. This is because as the forces are the vector quantity, the vector math is applied and the simplification is done.
13. The system of the collinear and the parallel force for the bodies over which this theorem is to be applied are simplified as:
a) The simplified collinear force system gives us a net force and the parallel force system gives us a simplified force, and then we add it vectorially
b) Such simplification is not possible
c) The simplification is usually done by not considering the directions of the both
d) The simplification is done by considering the rotations only
View Answer
Explanation: The simplification is easy. The simplified force system gives us a net force and the parallel force system gives us a simplified force, and then we add it vectorially. Thus the vector addition at the last can be easily done and thus both can be simplified.
14. If solving the question in 3D calculations is difficult, then use the 2D system to make the use of the theorem.
a) True
b) False
View Answer
Explanation: The answer is obviously yes. If we are having any difficulty in making the vector components, then we can go in 2D. As if the particle is in equilibrium, the net force will be zero. No matter where you see first. Net force is zero.
Sanfoundry Global Education & Learning Series – Engineering Mechanics.
To practice all areas of Engineering Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]