This set of Engineering Mechanics Multiple Choice Questions & Answers (MCQs) focuses on “Centroid of a Body”.
1. Density is best given by _______
a) Product of volume and density
b) Ratio of mass to Volume
c) Addition of mass and density
d) Subtraction of mass and density
View Answer
Explanation: The density is the ratio of the mass to the volume of the body. Thus arranging them and the volume is said to be a the ratio of mass to density. This equation is generally used in the calculations of the centroid of the body.
2. If solving the question in 3D calculations is difficult, then use the 2D system and then equate the ratio of the product of the centroid of the section to its mass to the total mass of the body to the centroid.
a) True
b) False
View Answer
Explanation: The answer is obviously no. Still, if we are having any difficulty in making the vector components, then we can go in 2D. As if the particle is in equilibrium, the net force will be zero. No matter where you see first. Net force is zero. But the statement here is not correct about the centroid.
3. One of the uses of the centroid is as in the simplification of the loading system the net force acts at the ___________ of the loading body.
a) Centroid
b) The centre axis
c) The corner
d) The base
View Answer
Explanation: In the simplification of the loading system the net force acts at the centroid of the loading body. That is if the loading system is in the form of the triangle then the at the distance 2 by 3 of the base the net force of the loading will act. And the load will be half the area of the loading.
4. The use of centroid comes in picture as if the non-Uniform loading is of the type of parabola then what will be the best suited answer among the following?
a) The net load will not be formed as all the forces will be cancelled
b) The net force will act the centre of the parabola
c) The net force will act on the base of the loading horizontally
d) The net force will act at the centroid of the parabola
View Answer
Explanation: The net force will act at the centroid of the parabola. Whether it be a parabola or the cubic curve the centroid is the only point at which the net force act. Force can’t be acted horizontally if the loading is vertical. Hence whatever be the shape of the loading, the centroid is the point of action of net force. Thus the use of centroid.
5. The x axis coordinate and the y axis coordinate of the centroid are having different types of calculations to calculate them.
a) True
b) False
View Answer
Explanation: The calculation is general to all the axis of the coordinate system. This means that the calculations are generalised for all the axis. All the axis are given the same priority. Thus no change in calculations.
6. The centre of ____________ is the ratio of the product of centroid and volume to the total volume.
a) Centroid axis
b) Density
c) Mass
d) Volume
View Answer
Explanation: The product of the centroid of the section to its volume to the total volume of the body is the centre of volume. Thus the answer. The ratio is generally used to locate the coordinate of the centroid or the centre of volume.
7. If the force vector F acting along the centroid is having its x-axis component being equal to Z N, y-axis component be X N and z-axis component be Y N then vector F is best represented by?
a) Xi + Yj + Zk
b) Yi + Xj + Zk
c) Zi + Yj + Xk
d) Zi + Xj + Yk
View Answer
Explanation: It is given that x, y and z-axis components are Z, X and Y respectively. Thus, just by placing the right coordinates we get option d to be correct. Here just the interchange of the axis’s representor with their respective axis is creating confusion. Which must be figured out.
8. Centroid of a body does depends upon the small weights of tiny particles. Which statement is right for force acting by the small particles of the body having it’s vector form as = Ai + Bj + Ck?
a) In rectangular components representation of any vector we have vector F = Ai + Bj + Ck
b) In rectangular components representation of any vector we have vector F = Ax + By + Cz
c) In rectangular components representation of any vector we have vector F = Fx + Fy + Fz
d) In rectangular components representation of any vector we have vector F = Fi + Fj + Fk
View Answer
Explanation: As given the vector is F = Ai + Bj + Ck, this implies that the x ,y and z-axis components of this vector is A, B and C respectively. But, in rectangular components representation of any vector, the vector is written as F = Fx + Fy + Fz.
9. Centroid determination involves the calculations of various forces. In that forces are having various properties. That is force is developed by a support that not allows the ________ of its attached member.
a) Translation
b) Rotation
c) Addition
d) Subtraction
View Answer
Explanation: The force developed by a support doesn’t allow the translation of its attached member. This is the basic condition for the equilibrium of the forces in any dimension. This rule is applied when the support reactions are taken into the account for the equilibrium of the body.
10. Determine the y coordinate of centroid of the area in the shape of circle as shown.
a) 4R/π
b) 2/π
c) 2R/3
d) 2R/5
View Answer
Explanation: The weight of the body is the sum of the all the small weights that are been applied by all the particles. The smaller the particle the smaller the weight it applies. Thus the total weight of the body is the summation of all the infinite number of small weights applied to the body.
11. What is not the condition for the equilibrium for the calculations used for the determination of the centroid in three dimensional system of axis?
a) ∑Fx=0
b) ∑Fy=0
c) ∑Fz=0
d) ∑F≠0
View Answer
Explanation: For the equilibrium in the three dimensional system of axis we have all the conditions true as, ∑Fx=0, ∑Fy=0 and ∑Fz=0. Also, we have the summation of the forces equal to zero. Which is not a non-zero value.
12. Determine the x coordinate of centroid of the area in the shape of circle as shown.
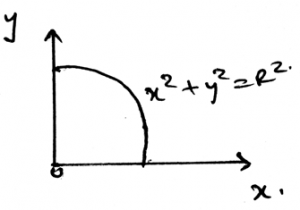
a) 4R/π
b) 2/π
c) 2R/3
d) 2R/5
View Answer
Explanation: The weight of the body is the sum of all the small weights that are been applied by all the particles. The smaller the particle the smaller the weight it applies. Thus the total weight of the body is the summation of all the infinite number of small weights applied to the body.
Sanfoundry Global Education & Learning Series – Engineering Mechanics.
To practice all areas of Engineering Mechanics, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
