This set of Engineering Mechanics Interview Questions and Answers focuses on “Addition of a System of Coplanar Forces”.
1. Which of the following statement is true?
a) A scalar is any physical quantity that can be completely specified by its magnitude
b) A vector is any positive or negative physical quantity that can be completely specified by its magnitude
c) A scalar is any physical quantity that requires both a magnitude and a direction for its complete description
d) A scalar is any physical quantity that can be completely specified by its direction
View Answer
Explanation: A scalar is any positive or negative physical quantity that can be completely specified by its magnitude. Examples of scalar quantities include length, mass, time, etc.
2. For two vectors defined by an arrow with a head and a tail. The length of each vector and the angle between them represents:
a) Their magnitude’s square and direction of the line of action respectively
b) Their magnitude and direction of the line of action respectively
c) Magnitude’s square root and direction of the line of action respectively
d) Magnitude’s square and the ratio of their lengths respectively
View Answer
Explanation: For two vectors defined by an arrow with a head and a tail. The length of each vector and the angle between them represents their magnitude and direction of the line of action respectively. The head/tip of the arrow indicates the sense of direction of the vector.
3. If a vector is multiplied by a scalar:
a) Then its magnitude is increased by the square root of that scalar’s magnitude
b) Then its magnitude is increased by the square of that scalar’s magnitude
c) Then its magnitude is increased by the amount of that scalar’s magnitude
d) You cannot multiply the vector with a scalar
View Answer
Explanation: If a vector is multiplied by a scalar then its magnitude is increased by the amount of that scalar’s magnitude. When multiplied by a negative scalar it going to change the directional sense of the vector.
4. All the vectors quantities obey:
a) Parallelogram law of addition
b) Parallelogram law of multiplication
c) Parallelogram law of addition of square root of their magnitudes
d) Parallelogram law of addition of square of their magnitudes
View Answer
Explanation: All the vectors quantities obey parallelogram law of addition. Two vectors A and B (can be called as component vectors) are added to form a resultant vector. R = A+B.
5. A force vector with magnitude R and making an angle α with the x-axis is having its component along x-axis and y-axis as:
a) Rcosine (α) and Rsine(α)
b) Rcosine (180-α) and Rsine(α)
c) Rcosine (180-α) and Rsine(180+α)
d) Rcosine (α) and Rsine(180+α)
View Answer
Explanation: The component along the x-axis is the cosine component of the vector. And the y-axis component of the vector is sine component, if the angle is being made with the x-axis. And 180- α for some of the trigonometric function may change their sign.
6. Dividing the X-axis component and the Y-axis component of the of the vector making an angle with Y-axis α will give us.
a) Cot α
b) Tan α
c) Sec α
d) 1
View Answer
Explanation: As the X-axis component of the vector becomes cos(90- α) and the Y-axis component becomes sin(90- α).Thus the division of both will give us Tan α.
7. Vector shown in the figure below have a length of 3m and the angles shown A and B are 60 and 30 degrees each. Calculate the X-axis and Y-axis components:
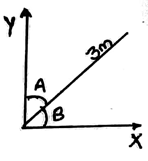
a) 2.59m and 1.50m respectively
b) 1.50m and 2.59m respectively
c) 3cos60 and 3sin30 respectively
d) 3sin60 and 3sin30 respectively
View Answer
Explanation: The sine and the cosine components of the given vectors considering the angle B as the only angle of consideration comes 1.5m and 2.59m.
8. Shown as in the figure below, A=60 degree and B=30 degree. Calculate the total length obtained by adding the x-axis component of both the vectors.
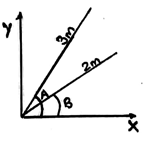
a) 3.23m
b) 4.35m
c) 2.50m
d) 1.5m
View Answer
Explanation: After getting the cosine components of the given vectors we obtain the total length of the x-axis components to be 3cos60 + 2cos30 = 3.23.
9. The magnitude of the resultant of the two vectors is always_____________
a) Greater than one of the vector’s magnitude
b) Smaller than one of the vector’s magnitude
c) Depends on the angle between them
d) Axis we choose to calculate the magnitude
View Answer
Explanation: Yes, the magnitude of the resultant of the two vectors always depends on the angle between them. It might be greater or smaller than one of the vector’s length. For perfectly saying, it does depend upon the angle between them.
10. If two equal vector forces are mutually perpendicular then the resultant force is acting at which angle as compared to one of the vector?
a) 45 degree
b) 90 degree
c) 180 degree
d) 0 degree
View Answer
Explanation: The vectors are mutually perpendicular, this means that the angle between the forces is 90 degree. Thus the resultant will form at 45 degrees to any of the vector.
11. What is the direction of the resultant vector if two vectors having equal length is placed in the Cartesian plane at the origin as, one being parallel to and heading towards positive x-axis and the other making 165 degree with it and heading in the opposite direction of that of the first one?
a) It is either in the 1st quadrant or in the 2nd quadrant
b) It is either in the 1st quadrant or in the 3rd quadrant
c) It is either in the 1st quadrant or in the 4th quadrant
d) Only in the 1st quadrant
View Answer
Explanation: If one is heading towards positive X-axis and the other is in the other direction opposite to the first one, with both having the same length and having an angle between them being obtuse, means that the direction is to be in the direction of either 1st quadrant or in the 4th quadrant.
12. Force vector R is having a______________
a) Length of R and a specific direction
b) Length of R
c) A specific direction
d) Length of magnitude equal to square root of R and a specific direction
View Answer
Explanation: As it is a force vector, it means it is going to have a direction and a magnitude. The magnitude is not the square root of R, R is just the magnitude of the vector given.
13. The resultant of three equal vectors having mutual angles being 120 degrees and being originated from a single point is zero.
a) True
b) False
View Answer
Explanation: As one can imagine three vectors coming out of a single point and are having a 120-degree angle with their adjacent ones, the resultant would be zero.
14. Every point on the force vector is having the same magnitude and the same direction as the whole force vector have.
a) True
b) False
View Answer
Explanation: The vector is made by joining the final and the starting point. If we consider any arbitrary point then the length would be calculated w.r.t the starting point, which might give different magnitude but same direction.
Sanfoundry Global Education & Learning Series – Engineering Mechanics.
To practice all areas of Engineering Mechanics for Interviews, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
