Microelectronics Questions and Answers - MOS Cascode - Set 2

This set of Microelectronics Multiple Choice Questions & Answers (MCQs) focuses on “MOS Cascode – Set 2”.

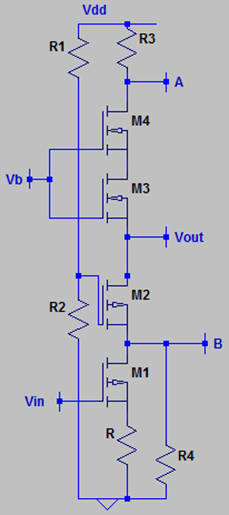
1. What is the impedance looking into the drain of M₃ in presence of channel length modulation & body effect?

a) [1+(g_mb3+g_m3)*r_o4)]*r_o4+r_o3
b) [1+(g_mb4+g_m4)*r_o3)]*r_o4+r_o3
c) [1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3
d) [1+(g_mb4*r_o3)]*r_o4+r_o3
View Answer

Answer: c
Explanation: M₃ is a PMOS and is degenerated by M₄. M₄ is also a PMOS and is degenerated by R₃ and it offers an output resistance of [1+(g_m4*r_o4)]*R₃+r_o4 to the source of M₃. Hence, the impedance looking into the drain terminal of M₃ will be [1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3. Note that the circuit below the drain terminal will not affect the impedance. This impedance can be verified by the small signal analysis.

2. What is the impedance looking into the drain of M₂ in presence of channel length modulation & body effect?

a) [1+(g_mb3*r_o4)]*r_o4+r_o3
b) [1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2
c) [1+(g_mb2*r_o2)]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2
d) [1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)]*R+r_o1)+r_o2
View Answer

Answer: b
Explanation: M₂ is a NMOS and is degenerated by M₁. M₁ is also a NMOS and is degenerated by R and it offers an output resistance of [{1+(g_m1*r_o1)}*R+r_o1 to the source of M₂. This impedance is in parallel to R₄. The total impedance degenerating M₂ is [1+(g_m1*r_o1)*R+r_o1]||R₄. Hence, the impedance looking into the drain terminal of M₃ will be [1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2. Note that the circuit above the drain terminal will not affect the impedance.

3. What is the output impedance of the following circuit if all the MOSFETs suffer from channel length modulation & body effect?

a) [1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o3]*([{1+(g_m2*r_o1)}*R+r_o2]||R₃)+r_o1
b) [1+(g_mb1*r_o1)]*([1+(g_m2*r_o4)]*R₂+r_o3)+r_o3||[1+((g_mb1+g_m2)*r_o4]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2
c) [1+(g_mb2*r_o3)]*([1+(g_m2*r_o3)]*R₄+r_o3)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2
d) [1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2
View Answer

Answer: d
Explanation: At the output node, we have primarily two branches. One branch is connected to a degenerated PMOS M₃, degenerated by M₄, which offers an output impedance of [1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3. Another branch is connected to a degenerated NMOS M₂, degenerated by a degenerated M₁, which offers an output impedance of [1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]|| R₄)+r_o2. These two impedance appear in parallel to each other and the overall output impedance is [1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2.

4. What is the transconductance of M₂ if all the MOSFETs suffers from Channel Length Modulation and body effect?
a) g_m2*r_o2/[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]+[1+(g_m2+g_mb2)[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]]r_o2
b) g_m1*r_o1/[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]+[1+(g_m4+g_mb4)[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]]r_o4
c) g_m2*r_o2/[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]+[1+(g_m3+g_mb3)[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]]r_o3
d) g_m3*r_o3/[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]+[1+(g_m1+g_mb3)[{1+(g_m1*r_o1)}*R+r_o1]||R₄]]r_o3
View Answer

Answer: a
Explanation: We know that in presence of channel length modulation, body effect and a source resistance – the transconductance of an NMOS or PMOS is g_m*r_o/R_S+[1+(g_m+g_mb)R_S]r_o. For M₂, the source resistance is R₄ in parallel to the output impedance of a degenerated M₁. This comes out to be ro1 [{1+(g_m1*r_o1)}*R+r_o1]||R₄. Henceforth, for M₂, the transconductance becomes g_m2*r_o2/[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]+[1+(g_m2+g_mb2)[[{1+(g_m1*r_o1)}*R+r_o1]||R₄]]r_o2. We can check the unit will come out to be Siemens and this can also be confirmed by a small signal analysis. Note that we are not concerned with the impedance connected to the drain of M₂ for now. In absence of body effect, we omit the g_mb terms.

5. What is the voltage gain of the following circuit if each MOSFET suffer from Channel Length Modulation & Body effect?

a) {(g_mb+g_m)*r_o+1}[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)] * R₃+r_o4) + r_o3||[1+(g_mb2+g_m2)*r_o2] * ([{1+(g_m1*r_o1)} * R++[[{1+(g_m1*r_o1)}*R+r_o1]]+[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2)]
b) {(g_mb+g_m)*r_o+1}[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)] * R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R++[[{1+(g_m1*r_o1)}*R+r_o1]]+[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+1)]
c) {(g_mb3+g_m1)*r_o+1}[[1+(g_mb2*r_o3)]*([1+(g_m4*r₀₄)] * R₃+r_o4)+r_o1]||R₄)+r_o2]/(r_o+(g_mb+g_m)*r_o[[{1+(g_m1*r_o1)}*R+r_o3]]+[[{1+(g_m1*r_o1)}*R+r_o1]]+[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o2)}*R+r_o1]||R₄)+r_o2)]
d) {(g_mb2+g_m2)*r_o2+1}[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)] * R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2] * ([{1+(g_m1*r_o1)} * R+r_o1]||R₄)+r_o2]/(r_o2+(g_mb2+g_m2)*r_o2[[{1+(g_m1*r_o1)}*R+r_o1]]+[[{1+(g_m1 * r_o1)}*R+r_o1]]+[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2)]
View Answer

Answer: d
Explanation: We analyze this circuit by observing that the output is taken from the drain of M₂ which behaves as a CG stage. In presence of Body effect and Channel Length modulation, the voltage gain of a CG stage is {(g_mb+g_m)*r_o+1}R_D/(r_o+(g_mb+g_m)*r_oR_S+R_S+R_D). Now, R_D is the total impedance connected to the drain of M₂ & it is the output impedance at the drain terminal. This resistance comes out to be [1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2]. Moreover, the source resistance is [{1+(g_m1*r_o1)}*R+r_o1]. Now, we simply replace R_D & R_S & the overall voltage gain comes out to be {(g_mb2+g_m2)*r_o2+1}[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2]/(r_o2+(g_mb2+g_m2)*r_o2[[{1+(g_m1*r_o1)}*R+r_o1]]+[[1+(g_mb3*r_o3)]*([1+(g_m4*r_o4)]*R₃+r_o4)+r_o3||[1+(g_mb2+g_m2)*r_o2]*([{1+(g_m1*r_o1)}*R+r_o1]||R₄)+r_o2)]. We note that the expression is very long & we can always use some approximations to calculate the voltage gain.

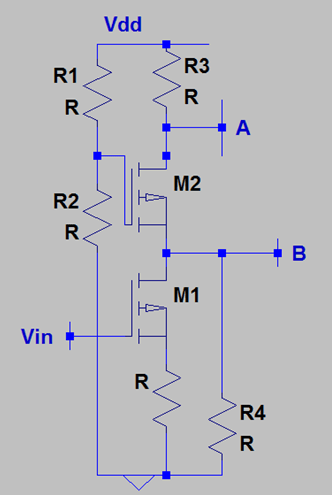
6. What is the voltage gain from node B to node A in presence of Channel Length Modulation & Body Effect?

a) {(g_m1+g_mb1)r_o1+1}/r_o2+(g_m2+g_mb1)*r_o2*([1+(g_m2+g_mb2)r_o1]R+r_o1||R₃)+([1+(g_m2-g_mb2)r_o1]R+r_o1||R₄)+R₃
b) {(g_m2+g_mb2)r_o2+1}/r_o2+(g_m2+g_mb2)*r_o2*([1+(g_m2+g_mb2)r_o1]R+r_o1||R₄)+([1+(g_m2+g_mb2)r_o1]R+r_o1||R₄)+R₃
c) {(g_m1+g_mb2)r_o2+1}/r_o1+(g_m1+g_mb2)*r_o2*([1+(g_m2+g_mb2)r_o1]R+r_o1||R₃)+([1+(g_m2-g_mb2)r_o1]R+r_o2||R₄)+R₃
d) {(g_m2+g_mb1)r_o1+1}/r_o1+(g_m2+g_mb2)*r_o2*([1+(g_m2+g_mb2)r_o1]R+r_o1||R₄)+([1+(g_m2+g_mb2)r_o1]R+r_o2||R₄)+R₃
View Answer

Answer: b
Explanation: From Node B to Node A, M₂ plays the role of a CG stage. The total resistance connected to the source of M₂ is a parallel combination of two impedances. The first is looking into the drain of M₁ which is degenerated by R and in presence of channel length modulation & body effect, it becomes [1+(g_m2+g_mb2)r_o1]R+r_o1. The second impedance is R₄. The overall impedance is [1+(g_m2+g_mb2)r_o1]R+r_o1||R₄. The total resistance connected to the drain of M₂ is R₃. From the expression of Voltage gain of a CG stage, in presence of channel length modulation & Body effect, the voltage gain is {(g_m2+g_mb2)r_o2+1}/r_o2+(g_m2+g_mb2)*r_o2*([1+(g_m2+g_mb2)r_o1]R+r_o1||R₄)+([1+(g_m2+g_mb2)r_o1]R+r_o1||R₄)+R₃. Note that in absence of body effect, only g_mb will disappear from the expression.

7. Which circuit is more linear?
Circuit: A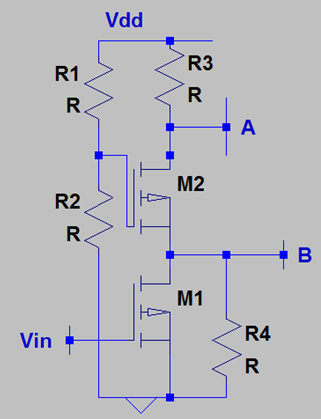 Ciruit: B
a) Circuit A
b) Circuit B
c) It depends on the biasing
d) It depends on the supply voltage
View Answer

Answer: b
Explanation: Circuit B is more linear than circuit A since both the MOSFETs are degenerated & degeneration leads to linearization of the circuit.

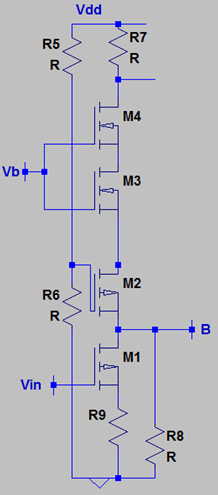
8. What is the role of M₄ in the following circuit?

a) Degenerating device
b) Input device
c) Amplifier
d) Error in the circuit
View Answer

Answer: a
Explanation: M₄ plays the role of a degenerating device. It is connected to the source of M₃ & it degenerates M₃ which leads to an increase in the impedance of M₃ which is seen looking into its drain terminal.

9. What is the voltage gain at Node B in presence of Channel length modulation and body effect in both the MOSFETs?

a) g_m1*r_o/R+[1+(g_m1+g_mb1)R]r_o1*(R₃+r_o2)/(1+(g_m2+g_mb2)*r_o2)||[1+(g_m2+g_mb2)r_o1]R+r_o1||R₄
b) g_m2*r_o/R+[1+(g_m2+g_mb2)R]r_o1*(R₃+r_o2)/(1+(g_m2+g_mb2)*r_o2)||[1+(g_m2+g_mb2)r_o1]R+r_o1||R₄
c) g_m1*r_o/R+[1+(g_m2+g_mb1)R]r_o1*(R₃+r_o2)/(1+(g_m2+g_mb2)*r_o2)||[1+(g_m2+g_mb2)r_o1]R+r_o1||R₄
d) g_m1*r_o/R+[1+(g_m1+g_mb1)R]r_o1*(R₃+r_o2)/(1+(g_m2+g_mb2)*r_o2)||[1+(g_m2+g_mb2)r_o1]R+r_o1||R₄
View Answer

Answer: d
Explanation: We analyze the circuit by observing that M₁ behaves as a CS stage. The transconductance of M₁ is g_m*r_o/R+[1+(g_m+g_mb)R]r_o1. The output impedance of is the parallel combination of the three impedances. The first impedance is looking into the source of M₂, which is (R₃+r_o2)/(1+(g_m2+g_mb2)*r_o2). The second is looking into the drain of M₁ which is degenerated by R and in presence of channel length modulation & body effect, it becomes [1+(g_m2+g_mb2)r_o1]R+r_o1. The final impedance is R₄. The overall output impedance is (R₃+r_o2)/(1+(g_m2+g_mb2)*r_o2)||[1+(g_m2+g_mb2)r_o1]R+r_o1||R₄ & the voltage gain becomes g_m1*r_o/R+[1+(g_m1+g_mb1)R]r_o1*(R₃+r_o2)/(1+(g_m2+g_mb2)*r_o2)||[1+(g_m2+g_mb2)r_o1]R+r_o1||R₄.

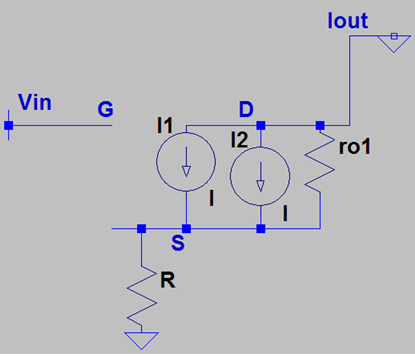
10. What is the transconductance of M₁ in presence of Channel Length Modulation & Body effect?

a) g_m2*r_o2/R+[1+(g_m2+g_mb1)R]r_o2
b) g_m1*r_o2/R+[1+(g_m2+g_mb2)R]r_o1
c) g_m1*r_o1/R+[1+(g_m1+g_mb1)R]r_o1
d) g_m2*r_o2/R+[1+(g_m1+g_mb2)R]r_o2
View Answer

Answer: c
Explanation: In order to calculate the transconductance of M₁, we analyze M₁ by neglecting M₂ since the current leaving the drain of M₁ is independent of R_D (the impedance of the branch connected to the drain terminal). Note that the voltage drop across R_D plays a role in establishing the region of operation but the transconductance i.e. ΔI_D/ΔV_GS is independent of R_D. We draw the small signal model of M₁ with channel length modulation and Body effect. Henceforth, we write a KCL at the source after noting that I₂=g_mb*V_S=g_mb*(I_OUT*R) & I₁=g_m*V_GS=g_m*(V_in-I_OUT*R) & I_ro1=V_S/r_o1=I_OUT*R/r_o1. The KCL revel as I_OUT=I₁–I₂–I_ro1 & we replace the terms and rearrange to find the transconductance as g_m*r_o/R+[1+(g_m+g_mb)R]r_o1.

Sanfoundry Global Education & Learning Series – Microelectronics.

To practice all areas of Microelectronics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Microelectronics Questions and Answers – MOS Cascode

» Next - Microelectronics Questions and Answers – Bipolar Cascode

Recommended Articles: