Bipolar Cascode - Microelectronics Questions and Answers

This set of Microelectronics Multiple Choice Questions & Answers (MCQs) focuses on “Bipolar Cascode”.

1. What is the input impedance of the following circuit?

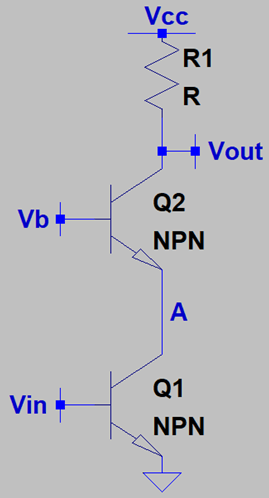
a) r_π1
b) r_π2 +r_π1
c) r_π2
d) Infinite
View Answer

Answer: a
Explanation: The input impedance of the circuit is simply r_π1. Q₂ doesn’t impact on the impedance and only the impedance looking into the base of Q₁ is the input impedance.

2. What is the input impedance of Q₂?

a) r_π1 + (β+1) * r_o2
b) r_π2 + (β+1) * r_o1
c) Infinite
d) 0
View Answer

Answer: b
Explanation: Q₂ is degenerated by the output impedance of Q₁, looking into its collector, i.e. r_o1. Henceforth, the input impedance becomes r_π2 + (β+1) * r_o1. This is directly derivable from the expression of input impedance of a degenerated B.J.T.

3. What is the impedance looking into the collector of Q₁ in the following circuit?

a) r_o2
b) r_o1+r_o2
c) r_o1
d) r_o1+r_π1
View Answer

Answer: c
Explanation: The impedance looking into the collector of Q₁ is independent of the rest of the circuit. This can be verified by a small signal analysis and hence, the impedance is r_o1.

4. What is the impedance looking into the collector of Q₂ in the following circuit?

a) (r_o2+R₁)*r_π2/(r_π1+(β+1)*r_O2+R₁)
b) (r_o1+R₁)*r_π1/(r_π2+(β+1)*r_O1+R₁)
c) (r_o1+R₁)*r_π2/(r_π1+(β+1)*r_O2+R₁)
d) (r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)
View Answer

Answer: d
Explanation: We draw the small signal model of Q₂ and readily note that V_X=-V_π and apply the Thevenin’s procedure of finding the resistance. Now, we apply a KCL at the collector node and find the current through r_o. This current is g_m*v_π+(I_X-V_X/r_π). Now, the current through R_C is I_X-V_X/r_π. Finally, we apply a KVL from V_IN, though r_o and R₁ to ground. After replacing the current and rearranging carefully, we reach the expression of impedance as (r_o2+R₁)*r_π2/(r_π2+(β+1)*r_o2+R₁). Note that we have calculated the input impedance of a CG stage with early effect.

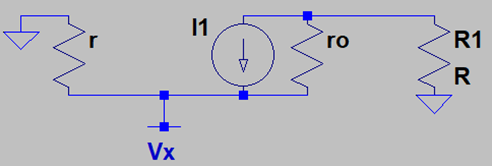
5. What is the impedance at node A if all the transistors experience early effect?

a) (r_o2+R₁)*r_π2/(r_π1+(β+1)*r_O1+R₁)||r_o1
b) (r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)||r_o1
c) (r_o1+R₁)*r_π1/(r_π2+(β+1)*r_O1+R₁)||r_o2
d) (r_o1+R₁)*r_π1/(r_π2+(β+1)*r_O2+R₁)||r_o2
View Answer

Answer: b
Explanation: At node A, we have two branches. One branch is connected to the emitter of Q₂ which gives an impedance as (r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁). The other branch is connected to the collector of Q₁ which gives a collector impedance of r_o2. When calculating the impedance, we turn off all the independent voltage sources and apply a voltage at node A. Henceforth, we find that the resistances offered by these two branches appear in parallel and the overall impedance becomes (r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)||r_o1.

6. What is the output impedance of the following circuit?

a) (1+g_m1*r_o1)(r_o2||r_π2)+r_o1||R₁
b) (1+g_m12*r_o1)(r_o2||r_π1)+r_o1||R₁
c) (1+g_m1*r_o2)(r_o1||r_π2)+r_o2||R₁
d) (1+g_m2*r_o2)(r_o2||r_π1)+r_o2||R₁
View Answer

Answer: d
Explanation: The output impedance of this circuit can be calculated by using the small signal analysis. We find that Q₂ is degenerated by the output impedance of Q₁ – the impedance looking into the collector of Q₁ becomes (1+g_m2*r_o2)(r_o2||r_π1)+r_o2. This impedance is parallel to R₁ and the overall impedance becomes (1+g_m2*r_o2)(r_o2||r_π1)+r_o2||R₁.

7. What is the transconductance of Q₁?

a) g_m1
b) g_m2
c) g_m1+g_m2
d) 0
View Answer

Answer: a
Explanation: The transconductance of Q₁ is only g_m1. Given the transistor is not degenerated, the transconductance remains g_m1.

8. What is the transconductance of Q₂?

a) g_m1
b) g_m2/1+g_m2*(r_o1)
c) g_m1+g_m2
d) g_m1/1+(1/r_π+g_m1*(r_o1))
View Answer

Answer: b
Explanation: The transconductance of a transistor reduces after it gets degenerated. The new transistor is g_m1/1+(1/r_π+g_m1*(degenerating resistance)). Therefore, for Q₂, the new transconductance is g_m1/1+(1/r_π+g_m1*(r_o1)). Note that option b is valid if the current gain is very high. Since it hasn’t been mentioned, we cannot take it as the correct answer.

9. What is the voltage gain from V_IN to node A in presence of Early Effect in all the transistors?

a) -g_m1*(r_o2+R₁)*r_π2/(r_π1+(β+1)*r_O1+R₁)||r_o2
b) -g_m2*(r_o1+R₁)*r_π1/(r_π2+(β+1)*r_O1+R₁)||r_o2
c) -g_m1*(r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)||r_o1
d) -g_m2*(r_o1+R₁)*r_π1/(r_π2+(β+1)*r_O2+R₁)||r_o1
View Answer

Answer: c
Explanation: The voltage gain from V_IN to node A is due to Q₁ behaving as a CS stage. The voltage gain of a CS stage is given by –(transconductance * (output impedance)). This impedance is given by the output impedance at node A. The output impedance is calculated as (r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)||r_o1. The overall gain is -g_m1*(r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)||r_o1.

10. What is the voltage gain node A to V_OUT in presence of early effect?

a) (1/r_o1+g_m1)(R₁||r_o1)
b) (1/r_o2+g_m2)(R₁||r_o2)
c) (1/r_o1+g_m2)(R₁||r_o1)
d) (1/r_o2+g_m1)(R₁||r_o2)
View Answer

Answer: b
Explanation: We draw the small signal model of Q₂ & neglect Q₁. Now, we calculate the current through r_o2 as V_IN-V_OUT/r_o2. Now, we write a KCL at the collector node and carefully rearrange the terms to get the voltage gain as (1/r_o2+g_m2)(R₁||r_o2).

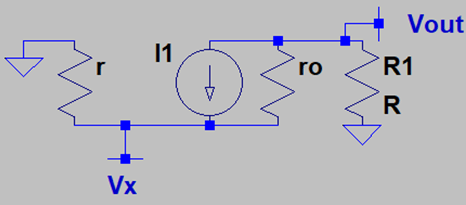
11. What is the voltage gain for the following circuit in presence of early effect?

a) -g_m1*(r_o1+R₁)*r_π1/(r_π1+(β+1)*r_O1+R₁)||r_o1*(1/r_o1+g_m2)(R₁||r_o1)
b) -g_m1*(r_o2+R₁)*r_π1/(r_π2+(β+1)*r_O2+R₁)||r_o2*(1/r_o2+g_m1)(R₁||r_o1)
c) -g_m1*(r_o1+R₁)*r_π2/(r_π1+(β+1)*r_O1+R₁)||r_o2*(1/r_o1+g_m1)(R₁||r_o2)
d) -g_m1*(r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)||r_o1*(1/r_o2+g_m2)(R₁||r_o2)
View Answer

Answer: d
Explanation: To calculate the voltage gain for the following circuit, we observe that V_OUT/V_IN=V_OUT/V_A*V_A/V_IN. Hence, we find that the overall voltage gain is the product of two voltage gain – one for Q₁ behaving as a CS stage and one for Q₂ behaving as a CG stage. For the CS stage, the gain is g_m1*(r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)||r_o1 while that of the CG stage is r_o1*(1/r_o2+g_m2)(R₁||r_o2). The overall voltage gain is the product of these two gains i.e. -g_m1*(r_o2+R₁)*r_π2/(r_π2+(β+1)*r_O2+R₁)||r_o1*(1/r_o2+g_m2)(R₁||r_o2).

12. What is the role of Q₂ in the following circuit?

a) Cascode Device
b) Degenerating Device
c) Follower
d) Driver
View Answer

Answer: a
Explanation: Q₂ is regarded as a Cascode Device. Q₂ is regarded as the degenerating device. None of the devices behave as a follower or driver since Q₂ behaves as a CG stage while Q₁ behaves as a CS stage.

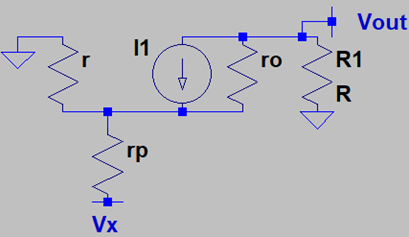
13. Suppose that a parasitic resistance appears in the emitter of Q₂. What happens to the voltage gain of the following circuit?

a) 1/(1/((r_o1+1/g_m1)(R₁||r_o1))+r_p/R₁
b) 1/(1/((r_o2+1/g_m1)(R₁||r_o1))+r_p/R₁
c) 1/(1/((r_o2+1/g_m2)(R₁||r_o2))+r_p/R₁
d) 1/(1/((r_o2+1/g_m1)(R₁||r_o2))+r_p/R₁
View Answer

Answer: c
Explanation: We draw the small signal model of Q₂ & neglect Q₁. Firstly, we perform a KVL from V_X to ground via r_p & r_π. Next, we note that the current leaving the emitter node and goes toward the collector is V_O/R₁. Hence, we can now define V_π in terms of V_in & V_out. Next, we perform a nodal analysis at the emitter node. Now, we note that the voltage gain from the emitter to V_OUT is (r_o2+1/g_m2)(R₁||r_o2). Henceforth, we replace the nodal voltage in terms of V_OUT & we can also replace V_π. After carefully rearranging the terms, we will get the voltage gain as 1/ (1/((r_o2+1/g_m2)(R₁||r_o2))+r_p/R₁.

Sanfoundry Global Education & Learning Series – Microelectronics.

To practice all areas of Microelectronics, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]

« Prev - Microelectronics Questions and Answers – MOS Cascode – Set 2

» Next - Microelectronics Questions and Answers – MOS Current Mirror

Recommended Articles: