This set of Machine Learning Multiple Choice Questions & Answers (MCQs) focuses on “Kernel Trick”.
1. When we make the half-space learning more expressive, the computational complexity of learning may increase.
a) False
b) True
View Answer
Explanation: Embedding the input space into some high dimensional feature space makes half-space learning more expressive. But the computational complexity of such learning may increase. So, computing linear separators over very high dimensional data may be computationally expensive.
2. Which of the following statements is not true about kernel?
a) Kernel is used to describe inner products in the feature space
b) The kernel function K specify the similarity between instances
c) The kernel function K specify the embedding as mapping the domain set into a space
d) The kernel function does the mapping of the domain set into a space where the similarities are realised as outer products
View Answer
Explanation: Mathematical meaning of a kernel is the inner product in some Hilbert space not the outer products. And it is a type of a similarity measure between instances. When we are embedding the data into a high dimensional feature space we introduce the idea of kernels.
3. Many learning algorithms for half-spaces can be carried out just on the basis of the values of the kernel function over pairs of domain points.
a) True
b) False
View Answer
Explanation: Many learning algorithms for half-spaces can be carried out just on the basis of the values of the kernel function over pairs of domain points. One of the main advantages of such algorithms is that they implement linear separators in high dimensional feature spaces without having to specify points in that space or expressing the embedding explicitly.
4. Which of the following statements is not true about the learning algorithms?
a) A feature mapping can be viewed as expanding the class of linear classifiers to a richer class
b) The suitability of any hypothesis class to a given learning task depends on the nature of that task
c) An embedding is a way to express and utilise prior knowledge about the problem at hand
d) The sample complexity required to learn with some kinds of kernels is independent of the margin in the feature space
View Answer
Explanation: Sample complexity required to learn with some kinds of kernels (Gaussian kernels) depends on the margin in the feature space which will be large, but can in general be arbitrarily small. All three other statements are true about learning algorithms.
5. A Hilbert space is a vector space with an inner product, which is also complete.
a) True
b) False
View Answer
Explanation: A Hilbert space is a vector space with an inner product, which is also complete. An inner product space X is called a Hilbert space if it is a complete metric space. And it is complete if all Cauchy sequences in the space converge. In feature mapping it maps the original instances into some Hilbert space.
6. The k degree polynomial kernel is defined as K(x, x’) = (1 + <x, x’>)k.
a) True
b) False
View Answer
Explanation: The k degree polynomial kernel is defined as K(x, x’) = (1 + <x, x’>)k where k is the degree of the polynomial. It is popular in image processing.
7. Which of the following statements is not true about kernel trick?
a) It allows one to incorporate prior knowledge of the problem domain
b) The training data only enter the algorithm through their entries in the kernel matrix
c) The training data only enter the algorithm through their individual attributes
d) The number of operations required is not necessarily proportional to the number of features
View Answer
Explanation: The training data only enter the algorithm through their entries in the kernel matrix (Gram matrix), and never through their individual attributes. All three are the advantages of kernel trick.
8. The Gaussian kernel is also called the RBF kernel, for Radial Basis Functions.
a) True
b) False
View Answer
Explanation: The Gaussian kernel is also called the RBF kernel, for Radial Basis Functions. RBF kernel is a kernel that is in the form of a radial basis function (more specifically, a Gaussian function). The RBF kernel is defined as : KRBF(x, x’) = exp[-ƴ ǁx – x’ǁ2].
9. Spectrum Kernel count the number of substrings in common.
a) True
b) False
View Answer
Explanation: Spectrum Kernel counts the number of substrings in common. It is a kernel since it is a dot product between vectors of indicators of all the substrings. Other kernels like: Gaussian kernel is a general-purpose kernel, Polynomial kernel is popular in image processing and sigmoid kernel can be used as the proxy for neural networks.
10. Which of the following statements is not true about kernel trick?
a) It provides a bridge from linearity to non-linearity to any algorithm that can expressed solely on terms of dot products between two vectors
b) If we first map the input data into a higher-dimensional space, a linear algorithm operating in this space will behave non-linearly in the original input space
c) The mapping is always need to be computed
d) If the algorithm can be expressed only in terms of an inner product between two vectors, all it need is replacing this inner product with the inner product from some other suitable space
View Answer
Explanation: Kernel trick is really interesting because that mapping does not need to be ever computed. That is where the trick resides, so wherever a dot product is used; it is replaced with a Kernel function. All other three statements best explain the kernel trick.
11. Which of the following statements is not true about kernel properties?
a) Kernel functions must be continuous
b) Kernel functions must be symmetric
c) Kernels which are said to satisfy the Mercer’s theorem are negative semi-definite
d) Kernel functions most preferably should have a positive (semi-) definite Gram matrix
View Answer
Explanation: Kernels which are said to satisfy the Mercer’s theorem are positive semi-definite as there is a property that kernel functions most preferably should have a positive (semi-) definite Gram matrix. And positive semi-definite means that their kernel matrices have only non-negative Eigen values.
12. Which of the following statements is not true about choosing the right kernel?
a) Linear kernel allows to picking out hyper spheres
b) A polynomial kernel allows to model feature conjunctions up to the order of the polynomial
c) Radial basis functions allow to pick out circles
d) Linear kernel allows picking out lines
View Answer
Explanation: A linear kernel allows only to picking out lines (hyper planes) and not to picking out hyper spheres (circles). Radial basis functions allow picking out circles and a polynomial kernel allows to model feature conjunctions up to the order of the polynomial.
13. As per the given figure Kernel trick illustrates some fundamental ideas about different ways to represent data and how machine learning algorithms see these different data representations.
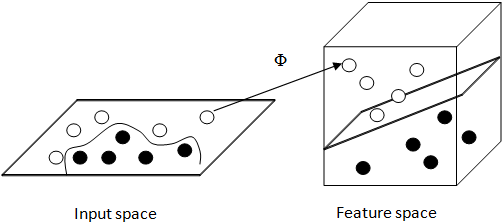
a) True
b) False
View Answer
Explanation: It is a kernel trick used in an SVM. Implementing support vector classifiers requires specifying a kernel function (Φ). Here in the picture the easily inseparable data is then transformed into a high dimensional feature space which is easily separable now using a kernel function. Kernel trick illustrates some fundamental ideas about different ways to represent data.
Sanfoundry Global Education & Learning Series – Machine Learning.
To practice all areas of Machine Learning, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
