This set of Machine Learning Multiple Choice Questions & Answers (MCQs) focuses on “Decision Trees – Gain Measure Implementation”.
1. Which of the following statements is not true about the Decision tree?
a) A Decision tree is also known as a classification tree
b) Each element of the domain of the classification in decision tree is called a class
c) It is a tree in which each internal node is labeled with an input feature
d) It cannot be used in data mining applications as it only classifies but not predicts anything
View Answer
Explanation: Decision trees can be widely used in data mining applications because it is able to classify and predict as well. It is also known as a classification tree. Each element of the domain of the classification in the decision tree is called a class and each internal node is labeled with an input feature.
2. Practical decision tree learning algorithms are based on heuristics.
a) True
b) False
View Answer
Explanation: Practical decision tree learning algorithms are based on heuristics such as a greedy approach, where the tree is constructed gradually, and locally optimal decisions are made at the construction of each node. Such algorithms cannot guarantee to return the globally optimal decision tree but tend to work reasonably well in practice.
3. Which of the following statements is not true about the Decision tree?
a) It starts with a tree with a single leaf and assign this leaf a label according to a majority vote among all labels over the training set
b) It performs a series of iterations and on each iteration, it examine the effect of splitting a single leaf
c) It defines some gain measure that quantifies the improvement due to the split
d) Among all possible splits, it either choose the one that minimizes the gain and perform it, or choose not to split the leaf at all
View Answer
Explanation: In decision trees among all the possible splits, it chooses the one that maximizes the gain not the one that minimizes it. Or it chooses not to split the leaf at all. All other three are the correct statements about the Decision tree.
4. Which of the following is not a Decision tree algorithm?
a) ID3
b) C4.5
c) DBSCAN
d) CART
View Answer
Explanation: DBSCAN is a clustering algorithm. ID3, C4.5, and CART are the Decision tree algorithms. ID3 is known as Iterative Dichotomiser 3 and C4.5 is the successor of ID3. CART is the Classification and Regression Tree. There are many other decision-tree algorithms also.
5. Which of the following statements is not true about the ID3 algorithm?
a) It is used to generate a decision tree from a dataset
b) It begins with the original set S as the root node
c) On each iteration of the algorithm, it iterates through every unused attribute of the set S and calculates the entropy or the information gain of that attribute
d) Finally it selects the attribute which has the largest entropy value
View Answer
Explanation: ID3 is an algorithm which is used to generate a decision tree from a dataset and it begins with the original set S as the root node. On each iteration of the algorithm, it iterates through every unused attribute of the set S and calculates the entropy or the information gain of that attribute. And it then selects the attribute which has the smallest entropy value.
6. Which of the following statements is not true about Information Gain?
a) It is a gain measure that is used in the ID3 algorithms
b) It is the difference between the entropy of the label before and after the split
c) It is based on the decrease in entropy after a data-set is split on an attribute
d) Constructing a decision tree is all about finding attribute that returns the lowest information gain
View Answer
Explanation: Information Gain is a measure that is used in the ID3 algorithms. Constructing a decision tree is all about finding the attribute that returns the highest information gain not the lowest one. It is the difference between the entropy of the label before and after the split.
7. Which of the following statements is not true about Information Gain?
a) It is the addition in entropy by transforming a dataset
b) It is calculated by comparing the entropy of the dataset before and after a transformation
c) It is often used in training decision trees
d) It is also known as Kullback-Leibler divergence
View Answer
Explanation: Information Gain is also known as Kullback-Leibler divergence which is the reduction in entropy by transforming a dataset. It is often used in training decision trees and is calculated by comparing the entropy of the dataset before and after a transformation.
8. Which of the following statements is not true about Information Gain?
a) It is the amount of information gained about a random variable or signal from observing another random variable
b) It tells us how important a given attribute of the feature vectors is
c) It implies how much entropy we removed
d) Higher Information Gain implies less entropy removed
View Answer
Explanation: The higher Information Gain implies more entropy removed not less because Information Gain implies how much entropy we removed. It tells us how important a given attribute of the feature vectors is. And it is the amount of information gained about a random variable or signal from observing another random variable.
9. Given the entropy for a split, Esplit = 0.39 and the entropy before the split, Ebefore = 1. What is the Information Gain for the split?
a) 1
b) 0.39
c) 0.61
d) 2.56
View Answer
Explanation: Information Gain is calculated for a split by subtracting the weighted entropies of each branch from the original entropy. We have Esplit = 0.39 and Ebefore = 1.
Then Information Gain, IG = Ebefore – Esplit
= 1 – 0.39
= 0.61
10. Which of the following statements is not an objective of Information Gain?
a) It tries to determine which attribute in a given set of training feature vectors is most useful for discriminating between the classes to be learned
b) Decision Trees algorithm will always tries to minimize Information Gain
c) It is used to decide the ordering of attributes in the nodes of a decision tree
d) Information Gain of certain event is the discrepancy of the amount ofinformation before someone observes that event and the amount after observation
View Answer
Explanation: Decision Trees algorithm will always try to maximize Information Gain. It tries to determine which attribute in a given set of training feature vectors is most useful for discriminating between the classes to be learned. And it is used to decide the ordering of attributes in the nodes of a decision tree.
11. Information Gain and Gini Index are the same.
a) True
b) False
View Answer
Explanation: Gini index measures the degree or probability of a particular variable being wrongly classified when it is randomly chosen. Unlike information gain, Gini Index is not computationally intensive as it doesn’t involve the logarithm function used to calculate entropy in information gain. So Gini Index is preferred over Information gain.
12. Which of the following statements is not true about Information Gain?
a) It is used to determine which feature/attribute gives us the maximum information about a class
b) It is based on the concept of entropy, which is the degree of impurity or disorder
c) It aims to reduce the level of entropy starting from the root node to the leave nodes
d) It is often promote the level of entropy starting from the root node to the leave nodes
View Answer
Explanation: Information Gain is based on the concept of entropy and it never tries to promote but tries to reduce the level of entropy starting from the root node to the leave nodes. All other options are true about Information Gain.
13. What is the entropy at P = 0.5 from the given figure?
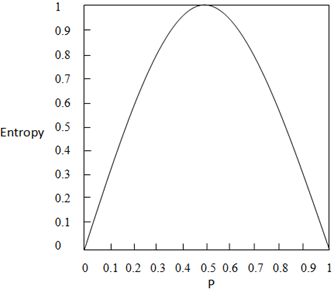
a) 0.5
b) -0.5
c) 1
d) -1
View Answer
Explanation: We know the entropy E = -p log2p – q log2q. Here p = 0.5 and q = 1 – p = 1 – 0.5 = 0.5. So we have p = 0.5 and q = 0.5.
Entropy = (-0.5 * log2 0.5) – (0.5 * log2 0.5)
= (-0.5 * -1) – (0.5 * -1)
= 0.5 + 0.5
= 1
14. Given entropy of parent = 1, weights averages = (\(\frac {3}{4}, \, \frac {1}{4}\)) and entropy of children = (0.9, 0). What is the information gain?
a) 0.675
b) 0.75
c) 0.325
d) 0.1
View Answer
Explanation: We know Information Gain = Entropy (Parent) – ∑(weights average * entropy (Child).
Information Gain = 1 – (\(\frac {3}{4}\) * 0.9 + \(\frac {1}{4}\) * 0)
= 1 – (0.675 + 0)
= 1 – 0.675
= 0.325
Sanfoundry Global Education & Learning Series – Machine Learning.
To practice all areas of Machine Learning, here is complete set of 1000+ Multiple Choice Questions and Answers.
If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]
