Compilers Questions and Answers – Obtaining the regular Expression from the Finite automata – 1

This set of Compilers Multiple Choice Questions & Answers (MCQs) focuses on “Obtaining the regular Expression from the finite automata – 1”.

1. L1 is accepted by the NFA, obtained by changing the accepting state of M to a non-accepting state and vice versa. Which of the following statements is true?

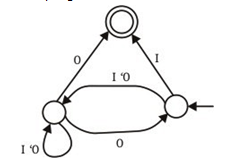
a) L1 = {0, 1}* – L
b) L1 = {0, 1}* – L
c) L1 ⊆ L
d) L1=L
View Answer

2. Given an arbitrary non-deterministic finite automaton (NFA) with N states, the maximum number of states in an equivalent minimized DFA is at least?
a) N²
b) 2^N
c) 2N
d) N!
View Answer

3. What can be said about a regular language L over {a} whose minimal finite state automaton has two states?
a) L must be {an| n is odd}
b) L must be {an| n is even}
c) L must be {an| n is even}
d) Either L must be {an | n is odd}, or L must be {an | n is even}
View Answer

4. How many minimum states are required to find whether a string has odd number of 0’s or not?
a) 1
b) 2
c) 3
d) 4
View Answer

Answer: b
Explanation: 2 minimum states are required to find whether a string has odd number of 0’s or not.

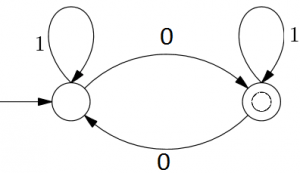
5. The number of states in DFA that accepts the language L(M) ∩ L(N) is _________

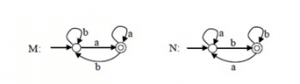
a) 0
b) 1
c) 2
d) 3
View Answer

Answer: b
Explanation: In DFA M: all strings must end with ‘a’. In DFA N: all strings must end with ‘b’. So the intersection is empty. For an empty language, only one state is needed.

6. Consider alphabet ∑ = {0, 1}, the null/empty string λ and the sets of strings X0, X1 and X0. How are X1 and X2 are related?

X0 = 1 X1
X1 = 0 X1 + 1 X2
X2 = 0 X1 + {λ} 

Which one of the following represents the strings in X0?
a) 10 (0* + (10)*)1
b) 10 (0* + (10)*)*1
c) 10 (0* + (10)*)*1
d) 10 (0 + 10)*1 + 110 (0 + 10)*1
View Answer

7. Which of the following languages is/are regular?

L1: {wxwR ⎪ w, x ∈ {a, b}* and ⎪w⎪, ⎪x⎪ >0} wR is the reverse of string w
L2: {anbm ⎪m ≠ n and m, n≥0}
L3: {apbqcr ⎪ p, q, r ≥ 0}  

a) L1 and L3 only
b) L2
c) L2 and L3 only
d) L3 only
View Answer

Answer: a
Explanation: L3 is simple to guess, it is regular.
Below is DFA for L1.

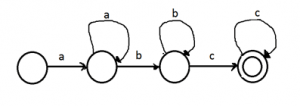
L1 is interesting. The important thing to note
about L1 is length of x is greater than 0.

8. The reorganizing capability of NDFA and DFA is?
a) May be different
b) Must be different
c) Must be same
d) None of the mentioned
View Answer

9. Which of the following is not regular?
a) String whose length is perfect square and consists of 0s
b) Palindromes consisting of 0’s and 1’s
c) String whose length is perfect square and consists of 0s & Palindromes consisting of 0’s and 1’s
d) None of the mentioned
View Answer

10. Which of the following pairs of regular expression are equivalent?
a) 1(01)* and (10)*1
b) X(xx)* and (xx)*x
c) 1(01)* and (10)*1 & X(xx)* and (xx)*x
d) None of the mentioned
View Answer

Sanfoundry Global Education & Learning Series – Compilers.

To practice all areas of Compilers, here is complete set of 1000+ Multiple Choice Questions and Answers.

If you find a mistake in question / option / answer, kindly take a screenshot and email to [email protected]