Theory of Computation – Conversion of Nondeterministic Finite Automata to Deterministic Finite Automata

For every nondeterministic finite automaton there exists an equivalent deterministic finite automaton. It means that for every nondeterministic finite automaton accepting a language L there exist a deterministic finite automaton that accepts the same language L. The DFA equivalent of an NFA simulates the moves of the NFA in parallel. To do that the states of the DFA will be a combination of one or more states of NFA. Hence every state of the DFA will be a subset of set of states of the NFA.

Algorithm

Let M₂ = {Q₂, Σ, δ₂, F₂, q’₀} be NFA that recognizes the language L and M = {Q, Σ, δ, F, q₀} be the corresponding DFA. To obtain the DFA we may proceed as follows:

1. Initially Q = Φ.
2. Put q’₀ into Q. q’₀ is the initial state of the DFA M.
3. Then for each q in Q do the following: add this new state, add δ(q, a) =U_pϵq δ₂(p, a) to δ. The state added to Q is a subset of states of NFA.
4. Repeat step 3 till new states are there to add in Q, the process terminates when there is no new state after step 3.

Note:The states added to Q with the final state of M₂ in the set of states are final states of the DFA.

Example: Convert the following NFA into DFA

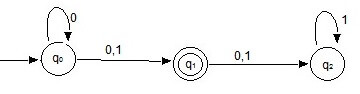
Solution

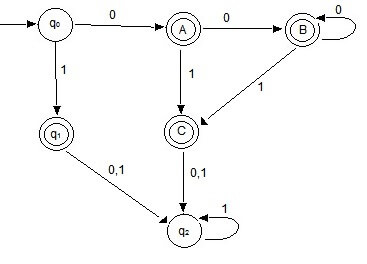
Sanfoundry Global Education & Learning Series – 100+ Theory of Computation Tutorials.

If you wish to look at all Tutorials and their examples, go to Theory of Computation Tutorials.