Arden’s Theorem
Let P and Q be two regular expressions over alphabet Σ. If P does not contain null string, then
R = Q + RP
has a unique solution that is R = QP*
Proof:
Put the value of R in the R.H.S.
R = Q + (Q + RP)P = Q + QP + RP2
When we put the value of R again and again we get the following equation
R = Q + QP + QP2 + QP3…..
R = Q(1 + P + P2 + P3 + ….
R = Q(є + P + P2 + P3 + ….
The second part of the product on the L.H.S can be replaced with the kleen closure. So the equation becomes
R = QP*
Using Arden’s Theorem to find Regular Expression of a Deterministic Finite automata
- For getting the regular expression for the automata we first create equations of the given form for all the states
q1 = q1w11 + q2w21 + … + qnwn1 + є (q1 is the initial state)
q2 = q1w12 + q2w22 + … + qnwn2
. .
. .
. .
qn = q1w1n + q2w2n + … + qnwnn
wij is the regular expression representing the set of labels of edges from qi to qj
Note: for parallel edges there will be that many expressions for that state in the expression. - Then we solve these equations to get the equation for qi in terms of wij and that expression is the required solution, where qi is a final state.
Assumptions made while forming the regular expression
- The transition diagram should not have є – transitions
- It must have only a single initial state
Let us see an example to demonstrate this method
Example: Draw a FA that accepts strings containing exactly 1 over alphabet {0, 1} and write a regular expression for the same.
View Answer
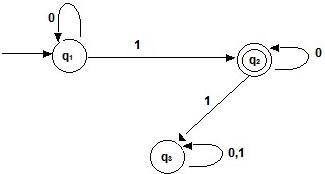
Now let us form the equation
q1 = q10 + є
q2 = q11 + q20
q3 = q21 + q30 + q31
Solving the equations
q1 = є0* (using Arden’s theorem; here Q = є , P = 0, R = q1)
q1 = 0*
q2 = 0*1 + q20
q2 = 0*1(0)* (here Q = 0*1, P = 0, R = q2)
Hence, 0*10* is the regular expression for the above deterministic finite automaton.
Note: We need not consider a trap state in our equations as it does not contribute to the regular expression
Given below are few questions for you to practice.
Question1: Construct a regular expression corresponding to the automata given below
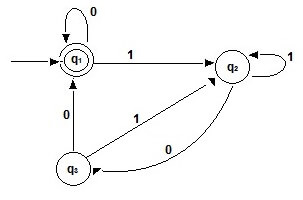
View Answer
q1 = q10 + q30 + є
q2 = q11 + q21 + q31
q3 = q20
Solving the equations
q2 = q11 + q21 + (q20)1 = q11 + q2(1 + 01)
q2 = q11 (1 + 01)*
So, q1 = q10 + q30 + є
q1= q10 + q11(1 + 01*)00 + є
= q1(0 + 1(1 + 01)*00) + є
= є (0 + 1(1 + 01)*00)*
q1=(0 + 1(1 + 01)*00)*
So the regular expression for the given automata is =(0 + 1(1 + 01)*00)*
View Answer
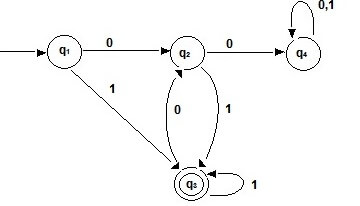
The equations for the above automata are:
q1 = є
q2 = q10 + q30
q3 = q11 + q21 + q3 1
Solving the above equations to get the regular expression
q2 = 0 + q30
q3 = 1 + 01 + q301 + q31
= (1 + 01) + q3(01 + 1)
q3 = (1 + 01) (1 + 01)*
(1 + 01)+ is the regular expression for the given language
Sanfoundry Global Education & Learning Series – 100+ Theory of Computation Tutorials.
If you wish to look at all Tutorials and their examples, go to Theory of Computation Tutorials.
If you find any mistake above, kindly email to [email protected]
- Check Automata Theory Books
- Apply for Computer Science Internship
- Check Computer Science Books
- Practice Computer Science MCQs
